
 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ)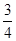 。
。 .
.  ·
· ·
· =
= .
.  =
= .
. =
=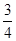 .
.  ,
,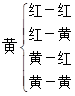 .
.  .
.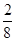 =
= .
.  =
=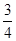 .
.

科目:高中数学 来源:不详 题型:解答题
| | 8环 | 9环 | 10环 |
| 甲 | 0.2 | 0.45 | 0.35 |
| 乙 | 0.25 | 0.4 | 0.35 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
. 元,该同学决定按
元,该同学决定按 顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试,试求该同学参加考试所需费用
顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试,试求该同学参加考试所需费用 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满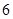 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 的分布列和数学期望
的分布列和数学期望 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 内的任意位置,如果通过大量的实验发现粒子落入△
内的任意位置,如果通过大量的实验发现粒子落入△ 内的频率稳定在
内的频率稳定在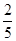 附近,那么点
附近,那么点 和点
和点 到时直线
到时直线 的距离之比约为( )
的距离之比约为( )
A.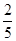 | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为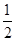 ,且各次投篮互不影响。(Ⅰ)求乙获胜的概率;(Ⅱ)求投篮结束时乙只投了2个球的概率。
,且各次投篮互不影响。(Ⅰ)求乙获胜的概率;(Ⅱ)求投篮结束时乙只投了2个球的概率。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com