
如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC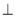 平面ABC.
平面ABC.
(1)证明:平面ACD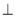 平面
平面 ;
;
(2)若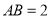 ,
,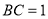 ,
,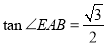 ,试求该简单组合体的体积V.
,试求该简单组合体的体积V.
(1)详见解析;(2)该简单几何体的体积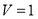 .
.
【解析】
试题分析:(1)欲证平面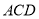 ⊥平面
⊥平面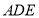 ,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面
,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面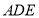 内找一条直线与平面
内找一条直线与平面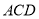 垂直,而由已知
垂直,而由已知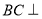 平面
平面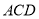 ,
,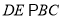 ,可得
,可得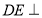 平面
平面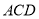 ,从而可得平面
,从而可得平面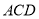 ⊥平面
⊥平面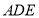 ;(2)所求简单组合体的体积进行分【解析】
;(2)所求简单组合体的体积进行分【解析】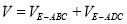 ,然后利用体积公式进行求解,关键是几何体的高的求解.
,然后利用体积公式进行求解,关键是几何体的高的求解.
试题解析:(1)证明:∵ DC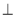 平面ABC ,
平面ABC ,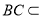 平面ABC
平面ABC
∴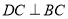 . .1分
. .1分
∵AB是圆O的直径 ∴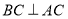 且
且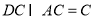
∴
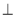 平面ADC. 3分
平面ADC. 3分
∵四边形DCBE为平行四边形 ∴DE//BC
∴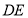
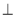 平面ADC 5分
平面ADC 5分
又∵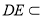 平面ADE ∴平面ACD
平面ADE ∴平面ACD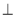 平面
平面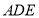 ..6分
..6分
(2)所求简单组合体的体积: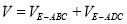
∵ ,
,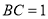 ,
, 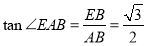
∴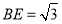 ,
,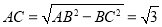 10分
10分
∴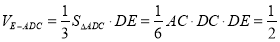
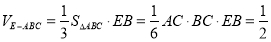
∴该简单几何体的体积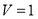 12分
12分
考点:平面与平面垂直的判定;棱柱、棱锥、棱台的体积.


科目:高中数学 来源:2013-2014学年江西省盟校高三第二次联考文科数学试卷(解析版) 题型:选择题
对于实数 和
和 ,定义运算
,定义运算 ,运算原理如右图所示,则式子
,运算原理如右图所示,则式子 的值为( )
的值为( )
A.6 B.7 C.8 D.9

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考理科数学试卷(解析版) 题型:选择题
给出下列命题,其中真命题的个数是( )
①存在 ,使得
,使得 成立;
成立;
②对于任意的三个平面向量 、
、 、
、 ,总有
,总有 成立;
成立;
③相关系数 (
( ),
), 值越大,变量之间的线性相关程度越高.
值越大,变量之间的线性相关程度越高.
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟理科数学试卷(解析版) 题型:填空题
执行下图所示的程序框图,若输入A=2014,B=125,输出的A的值是____ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com