
| A. | $(0,\frac{1}{2})∪(2,+∞)$ | B. | $(\frac{1}{2},1)∪(2,+∞)$ | C. | (2,+∞) | D. | $(\frac{1}{2},1)$ |
分析 由当x∈[0,+∞)时,f(x)=2x-2,可得:f(x)为增函数,又由f(x)定义在R上的偶函数,可得:f(x)>0时,x>1,或x<-1,故f(log2x)>0时,log2x>1,或log2x<-1.
解答 解:当x∈[0,+∞)时,f(x)=2x-2,
∴f(1)=0,
又∵当x∈[0,+∞)时,f(x)为增函数,又是定义在R上的偶函数,
故f(x)>0时,x>1,或x<-1,
故f(log2x)>0时,log2x>1,或log2x<-1,
解得:x∈(0,$\frac{1}{2}$)∪(2,+∞),
故选A.
点评 本题考查的知识点是对数函数的单调性与特殊点,指数函数的单调性,函数的奇偶性,难度中档.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:解答题
| 专业对口 | 专业不对口 | 合计 | |
| 男 | 30 | 10 | 40 |
| 女 | 35 | 5 | 40 |
| 合计 | 65 | 15 | 80 |
| P(K) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.306 | 3.841 | 5.021 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
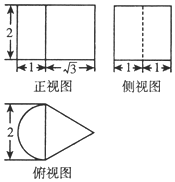
| A. | $\frac{2\sqrt{3}}{3}$+π | B. | $\frac{2\sqrt{3}}{3}$+2π | C. | 2 $\sqrt{3}$+2π | D. | 2 $\sqrt{3}$+π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2 | B. | loga2 | C. | 2 | D. | loga(loga2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com