练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知（）.
    ⑴求的单调区间；
    ⑵若在内有且只有一个极值点, 求a的取值范围.

    ⑴①当时，在和单调递增，在单调递减；②当时，单调递增；
    ⑵.

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    函数在一个周期内的图象如图所示，为图象的最高点，、为图象与轴的交点，且为正三角形。

    （Ⅰ）求的值及函数的值域；
    （Ⅱ）若，且，求的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    已知是函数图象的一条对称轴．
    （Ⅰ）求的值；
    （Ⅱ）作出函数在上的图象简图（不要求书写作图过程）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题12分）设.向量.
    (Ⅰ) 当时,求函数的值域;
    (Ⅱ)当时,求函数的单调递减区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分12分）已知函数（其中的最小正周期为.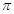
    （Ⅰ）求的值，并求函数的单调递减区间；
    （Ⅱ）在锐角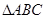中，分别是角的对边，若
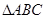    的面积为，求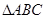的外接圆面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分13分）
    （Ⅰ）已知扇形的面积为，弧长为，求该扇形的圆心角（用弧度制表示）；
    （Ⅱ）在平面直角坐标系中，角的终边在直线上，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分13分)
    已知三点A（3，0），B（0，3），C，．
    （1）若，求角；
    （2）若，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在中，，，分别是三内角A，B，C所对的三边，已知．
    （1）求角A的大小；
    （2）若，试判断的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （1）已知函数，求函数在区间上的单调增区间；
    （2）计算：.

    查看答案和解析>>

    同步练习册答案