
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
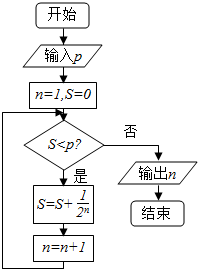
分析 由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量n的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:根据流程图所示的顺序,
该程序的作用是判断S=$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n}}$>0.95时,n+1的值.
当n=2时,$\frac{1}{2}$+$\frac{1}{4}$=0.75<0.95,
当n=3时,$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$=0.875<0.95,
当n=4时,$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$=0.9375<0.95,
当n=5时,$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$=0.96875>0.95,
此时n+1=6.
则输出的n=6
故选:C
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | ab<b2 | C. | a+b<0 | D. | |a|+|b|>|a+b| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | π | C. | π2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
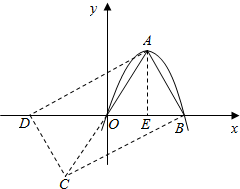 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com