
���� ��1����A��m��n����m��0��n��0����sin��A F1F2=$\frac{1}{\sqrt{5}}$���ɵ�tan��AF1F2=$\frac{1}{2}$��$\frac{n}{m+c}$=$\frac{1}{2}$����sin��A F1F2=$\frac{1}{\sqrt{5}}$��cos��F1AF2=$\frac{4}{5}$��tan��AF2F1=-2�ɵ�$\frac{n}{m-c}$=2���ɡ�AF1F2�����Ϊ1�ɵ�$\frac{1}{2}$•2c•n=1���������A�����꣬���ɵó�˫���ߵķ��̣�
��2��ֱ����˫���߷��������������б�ʽ����0��������ʵ��k��ȡֵ��Χ��
��� �⣺��1����A��m��n����m��0��n��0��
��sin��A F1F2=$\frac{1}{\sqrt{5}}$���ɵ�tan��AF1F2=$\frac{1}{2}$��$\frac{n}{m+c}$=$\frac{1}{2}$��
��sin��A F1F2=$\frac{1}{\sqrt{5}}$��cos��F1AF2=$\frac{4}{5}$��tan��AF2F1=-2�ɵ�$\frac{n}{m-c}$=2��
�ɡ�AF1F2�����Ϊ1�ɵ�$\frac{1}{2}$•2c•n=1��
������ʽ������ã�c=$\frac{\sqrt{3}}{2}$��m=$\frac{5\sqrt{3}}{6}$��n=$\frac{2\sqrt{3}}{3}$��
����A��$\frac{5\sqrt{3}}{6}$��$\frac{2\sqrt{3}}{3}$����F1��-$\frac{\sqrt{3}}{2}$��0����F2��$\frac{\sqrt{3}}{2}$��0����
����˫���߶���ɵ�2a=|AF1|-|AF2|=$\frac{\sqrt{15}}{3}$��
����a=$\frac{\sqrt{15}}{6}$��b=$\frac{1}{3}$��
����˫���߷���Ϊ$\frac{12{x}^{2}}{5}-3{y}^{2}$=1��
��2��ֱ��y=kx+1��˫���߷��������ɵã�12-15k2��x2-30kx-20=0��
��ֱ��y=kx+1��˫�����ཻ�ڲ�ͬ���㣬���=900k2+80��12-15k2����0����-$\frac{4\sqrt{5}}{5}$��k��$\frac{4\sqrt{5}}{5}$��
���� ������Ҫ����˫���߷��̣�������˫���ߵļ����ʣ�������ѧ����˫������֪ʶ�������������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-16��0] | B�� | [0��16] | C�� | [-4��20] | D�� | [-20��4] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

| PM2.5��ƽ��Ũ�ȣ���/�����ף� | [0��20] | ��20��40] | ��40��60] | ��60��80] | ��80��100] |
| Ƶ�����죩 | 2 | 3 | 4 | 6 | 5 |
| ����ȵȼ� | �dz����� | ���� | ������ |
| PM2.5��ƽ��Ũ�ȣ���/�����ף� | ������20 | ����20������60 | ����60 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
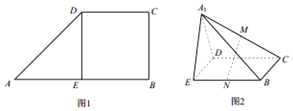 ��ͼ1����ֱ������ABCD�У�AB��CD��AB��BC��AB=2CD��DE��AB����DE����AEDD����A1ED��λ�ã�����A1B��A1C��M��N�ֱ�ΪA1C��BE���е㣮��ͼ2��
��ͼ1����ֱ������ABCD�У�AB��CD��AB��BC��AB=2CD��DE��AB����DE����AEDD����A1ED��λ�ã�����A1B��A1C��M��N�ֱ�ΪA1C��BE���е㣮��ͼ2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com