练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数y=ex•sinx+1在点（π，1）处的切线方程是
    ex+y-πex-1=0
    ex+y-πex-1=0
    ．
    分析：先求导函数，进而可以求切线斜率，从而可求切线方程．
    解答：解：由题意，y′=exsinx+excosx
    当x=π时，y′=-eπ
    ∴函数y=ex•sinx+1在点（π，1）处的切线方程是y-1=-eπ（x-π）
    即xeπ+y-1-πeπ=0
    故答案为 xeπ+y-1-πeπ=0
    点评：本题以函数为载体，考查导数的几何意义，考查切线方程．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在技术工程上，常用到双曲线正弦函数sinhx=
    ex-e-x
    2
    和双曲线余弦函数coshx=
    ex+e-x
    2
    ，而双曲线正弦函数和双曲线余弦函数与我们学过的正弦函数和余弦函数有许多类似的性质，比如关于正、余弦函数有sin（x+y）=sinxcosy+cosxsiny成立，而关于双曲正、余弦函数满足sh（x+y）=shxchy+chxshy．请你运用类比的思想，写出关于双曲正弦、双曲余弦的一个新关系式
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列四个命题：
    ①命题“?x∈R，ex＞x”的否定是““?x∈R，ex＜x”
    ②将函数y=sin(2x+
    π
    3
    )    的图象向右平移
    π
    3
    个单位，得到函数y=sin2x的图象；
    ③用数学归纳法证明（n+1）（n+2）…（n+n）=2n•1•3…（2n-1）（n∈N*）时，从“k”到“k+1”的证明，左边需增添的一个因式是2（2k+1）；
    ④函数f（x）=ex-x-1（x∈R）有两个零点．
    其中所有真命题的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

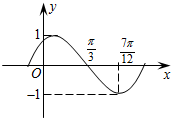    （2011•静海县一模）已知下列四个命题：
    ①i是虚数单位，则
    2i3
    1-i
    =1-i；
    ②命题“存在x0∈R，2x0≤0”的否定是“不存在x0∈R，2x0＞0”；
    ③函数f（x）=ex+x-2在区间（0，1）内有零点；
    ④函数y=sin（ωx+φ）（ω＞0，|φ|＜
    π
    2
    ）的图象的一部分如图所示，则ω、φ的值分别为2，-
    π
    3
    ．
    其中是真命题的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：河南省许昌市第二高级中学2011届高三第一次月考理科数学试题 题型：022

    给出下列四个命题：

    ①命题“x∈R，ex＞x”的否定是“x∈，ex＜x”

    ②将函数y＝sin(2x＋)的图象向右平移个单位，得到函数y＝sin2x的图象；

    ③用数学归纳法证明(n＋1)(n＋2)…(n＋n)＝2n·1·3…(2n－1)(n∈N*)时，从“k”到“k＋1”的证明，左边需增添的一个因式是2(2k＋1)；

    ④函数f(x)＝ex－x－1(x∈R)有两个零点．其中所有真命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题正确的是                                                    (　　)

    A．函数y＝的图像关于点(2，－1)对称

    B．将函数y＝sin(x－)的图像向右平移个单位可得函数y＝sinx的图像

    C．函数y＝－ex与y＝e－x的图像关于原点对称

    D．函数y＝a－x与y＝loga(－x)(a>0且a≠1)的图像关于直线y＝x对称

    查看答案和解析>>

    同步练习册答案