
【题目】已知函数 ![]() .
.
(1)求函数f(x)的单调增区间;
(2)若直线y=a与函数f(x)的图象无公共点,求实数a的取值范围.
【答案】
(1)解:函数 ![]() =cosx(
=cosx( ![]() cosx+
cosx+ ![]() sinx)
sinx)
= ![]() +
+ ![]() sin2x=
sin2x= ![]() cos(2x﹣
cos(2x﹣ ![]() )+
)+ ![]() ,
,
由2kπ﹣π≤2x﹣ ![]() ≤2kπ,k∈Z,
≤2kπ,k∈Z,
解得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
即f(x)的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z;
],k∈Z;
(2)解:由(1)可得当2x﹣ ![]() =2kπ,即x=kπ+
=2kπ,即x=kπ+ ![]() ,k∈Z时,f(x)取得最大值
,k∈Z时,f(x)取得最大值 ![]() ;
;
当2x﹣ ![]() =2kπ+π,即x=kπ+
=2kπ+π,即x=kπ+ ![]() ,k∈Z时,f(x)取得最小值﹣
,k∈Z时,f(x)取得最小值﹣ ![]() .
.
由直线y=a与函数f(x)的图象无公共点,
可得a的范围是a> ![]() 或a<﹣
或a<﹣ ![]() .
.
【解析】(1)运用两角差的余弦公式和二倍角公式,化简可得f(x),再由余弦函数的单调区间,解不等式可得所求增区间;(2)求得f(x)的最值,即可得到a的取值范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=xex﹣ax2﹣x,a∈R.
(1)当a= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)若对x≥1时,恒有f(x)≥xex+ax2成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2(a为实常数).
(1)当a=﹣4时,求函数f(x)在[1,e]上的最大值及相应的x值;
(2)当x∈[1,e]时,讨论方程f(x)=0根的个数.
(3)若a>0,且对任意的x1 , x2∈[1,e],都有 ![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
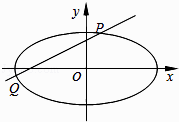
【题目】已知中心在原点O,焦点在x轴上,离心率为 ![]() 的椭圆过点(
的椭圆过点( ![]() ,
, ![]() ).
). 
(1)求椭圆的方程;
(2)设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1. 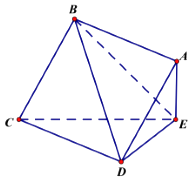
(1)求证:AB∥平面CDE;
(2)求证:DE⊥平面ABE;
(3)求点A到平面BDE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差为2,前n项和为Sn , 且S1、S2、S4成等比数列.
(1)求数列{an}的通项公式;
(2)令bn=(﹣1)n﹣1 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥V﹣ABCD中,底面ABCD是边长2为的正方形,其他四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形. 
(1)求正四棱锥V﹣ABCD的体积.
(2)求二面角V﹣BC﹣A的平面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com