
如图①,△BCD内接于直角梯形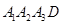 ,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
(1)求证:AB⊥CD;
(2)求直线BD和平面ACD所成的角的正切值;
(3)求四面体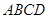 的体积。
的体积。
(1)详见解析;(2) 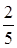 ; (3)
; (3) 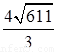
【解析】
试题分析:(1)平面图中因为A1D∥A2A3,A1A2⊥A2A3,所以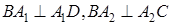 ,立体图中不变,即
,立体图中不变,即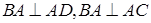 ,可证得
,可证得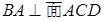 ,就可证出AB⊥CD。(2)由(1)知AB⊥平面ACD.,所以AD即为BD在面ACD内的射影,所以∠BDA即为所求。在直角三角形中利用三角函数可求其正切值。(3)由(1)知
,就可证出AB⊥CD。(2)由(1)知AB⊥平面ACD.,所以AD即为BD在面ACD内的射影,所以∠BDA即为所求。在直角三角形中利用三角函数可求其正切值。(3)由(1)知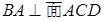 ,所以可以选以面ADC为底面,以AB为高求其体积。
,所以可以选以面ADC为底面,以AB为高求其体积。
试题解析:(1)证明:∵在直角梯形A1A2A3D中,A1B⊥A1D,A2B⊥A2C,
∴在三棱锥ABCD中,AB⊥AD,AB⊥AC.
∵AC∩AD=A,∴AB⊥平面ACD.
∵CD⊂平面ACD,∴AB⊥CD.
(2)解:由(1)知AB⊥平面ACD,
∴AD为BD在平面ACD内的射影,
∠BDA是直线BD和平面ACD所成的角.
依题意,在直角梯形A1A2A3D中,
A1D=A3D=10,A1B=A2B=4,
∴在三棱锥ABCD中,AD=10,AB=4.
在Rt△ABD中,tan ∠BDA=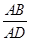 =
=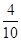 =
=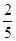 .
.
∴直线BD和平面ACD所成的角的正切值为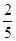 .
.
(3)由(2)得: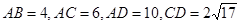
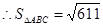
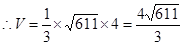
考点:线面垂直证线线垂直,线面角,多面体体积。


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源:2012-2013学年广东省东莞市高三(上)期末数学试卷(文科)(解析版) 题型:填空题
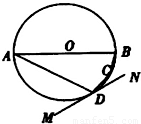
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省肇庆市广宁中学高三(下)2月月考数学试卷(文科)(解析版) 题型:填空题
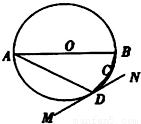
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com