
【题目】已知函数![]() ,
,![]() (
(![]() 是
是![]() 的导函数),
的导函数),![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在
在![]() 内的极值点个数,并加以证明.
内的极值点个数,并加以证明.
【答案】(1)![]() (2)
(2)![]() 在
在![]() 上共有两个极值点,详见解析
上共有两个极值点,详见解析
【解析】
(1)先求得![]() ,再求得
,再求得![]() ,再讨论
,再讨论![]() 的符号,判断函数
的符号,判断函数![]() 的单调性,再求最值即可得解;
的单调性,再求最值即可得解;
(2)利用(1)的结论,结合![]() ,
,![]() ,由零点定理可
,由零点定理可![]() 在
在![]() 上有且仅有一个变号零点;再当
上有且仅有一个变号零点;再当![]() 时,由导数的应用可
时,由导数的应用可![]() 使
使![]() ,即
,即![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,再结合特殊变量所对应的函数值的符号可得
上单调递减,再结合特殊变量所对应的函数值的符号可得![]() 在
在![]() 上有且仅有一个变号零点,综合即可得解.
上有且仅有一个变号零点,综合即可得解.
解:(1)由![]()
则![]() ,
,
则![]() ,
,
①当![]() 时
时![]() ,不合题意,舍去.
,不合题意,舍去.
②当![]() 时
时![]() ,∴
,∴![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,不合题意,舍去.
,不合题意,舍去.
③当![]() 时
时![]() ,∴
,∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,解得
,解得![]() ,
,
∴综上:![]() .
.
(2)由(Ⅰ)知![]() ,
,![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]() ,
,
∴![]() 在
在![]() 上有且仅有一个变号零点;
上有且仅有一个变号零点;
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,![]() ,
,
∴![]() 使
使![]() 且当
且当![]() 时
时![]() ,当
,当![]() 时
时![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
又![]() ,
,![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上有且仅有一个变号零点.
上有且仅有一个变号零点.
∴![]() 在
在![]() 和
和![]() 上各有一个变号零点,∴
上各有一个变号零点,∴![]() 在
在![]() 上共有两个极值点.
上共有两个极值点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】众所周知,城市公交车的数量太多会造成资源的浪费,太少又难以满足乘客的需求,为此,某市公交公司在某站台的50名候车乘客中随机抽取10名,统计了他们的候车时间(单位:分钟),得到下表.
候车时间 | 人数 |
| 1 |
| 4 |
| 2 |
| 2 |
| 1 |
(1)估计这10名乘客的平均候车时间(同一组中的每个数据可用该组区间的中点值代替);
(2)估计这50名乘客的候车时间少于10分钟的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD为正方形,![]() ,E,F分别是棱PC,AB的中点.
,E,F分别是棱PC,AB的中点.
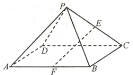
(1)求证:![]() 平面PAD;
平面PAD;
(2)若![]() ,求直线EF与平面PAB所成角的正弦值.
,求直线EF与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
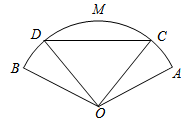
【题目】如图,有一块半径为20米,圆心角![]() 的扇形展示台,展示台分成了四个区域:三角形
的扇形展示台,展示台分成了四个区域:三角形![]() ,弓形
,弓形![]() ,扇形
,扇形![]() 和扇形
和扇形![]() (其中
(其中![]() ).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米
).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米![]() ,紫龙卧雪30元/米
,紫龙卧雪30元/米![]() ,朱砂红霜40元/米
,朱砂红霜40元/米![]() .
.
(1)设![]() ,试建立日效益总量
,试建立日效益总量![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)试探求![]() 为何值时,日效益总量达到最大值.
为何值时,日效益总量达到最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某地区年龄在25~55岁的人员中,随机抽出100人,了解他们对今年两会的热点问题的看法,绘制出频率分布直方图如图所示,则下列说法正确的是( )

A. 抽出的100人中,年龄在40~45岁的人数大约为20
B. 抽出的100人中,年龄在35~45岁的人数大约为30
C. 抽出的100人中,年龄在40~50岁的人数大约为40
D. 抽出的100人中,年龄在35~50岁的人数大约为50
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将甲、乙、丙、丁四个人安排到座位号分别是![]() 的四个座位上,他们分别有以下要求,
的四个座位上,他们分别有以下要求,
甲:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
乙:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
丙:我的要求和乙一样;
丁:如果乙不坐座位号为![]() 的座位,我就不坐座位号为
的座位,我就不坐座位号为![]() 的座位.
的座位.
那么坐在座位号为![]() 的座位上的是( )
的座位上的是( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com