
(本小题满分12分)在锐角△ABC中, 分别为∠A、∠B、∠C所对的边,且
分别为∠A、∠B、∠C所对的边,且
(1)确定∠C的大小;
(2)若c= ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
(1)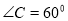 或
或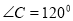 ;(2)
;(2) .
.
【解析】
试题分析:(1)利用正弦定理,将边角关系转化为角角关系进行求解;(2)利用正弦定理用角A的三角函数表示,利用三角函数的图像与性质进行求解.
解题思路: 解三角形问题,要灵活选用正弦定理、余弦定理、三角形的面积公式和内角和定理进行求解,还往往与两角和的三角公式相联系.
试题解析:(1)已知a、b、c分别为∠A、∠B、∠C所对的边,由 a=2csinA,
a=2csinA,
得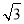 sinA=2sinCsinA,又sinA≠0,则sinC=
sinA=2sinCsinA,又sinA≠0,则sinC=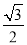 ,∴∠C=60°或∠C=120°,
,∴∠C=60°或∠C=120°,
∵△ABC为锐角三角形,∴∠C=120°舍去。∴∠C=60°
(2)∵c= ,sinC=
,sinC=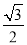
∴由正弦定理得: ,
,
即a=2sinA,b=2sinB,又A+B=π-C=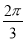 ,即B=
,即B=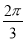 -A,
-A,
∴a+b+c=2(sinA+sinB)+
=2[sinA+sin(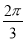 -A)]+
-A)]+ 
=2(sinA+sin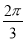 cosA-cos
cosA-cos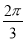 sinA)+
sinA)+
=3sinA+ cosA+
cosA+
=2 (sinAcos
(sinAcos +cosAsin
+cosAsin )+
)+
=2 sin(A+
sin(A+ )+
)+ ,
,
∵△ABC是锐角三角形,
∴ <∠A<
<∠A< ,∴
,∴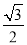 <sin(A+
<sin(A+ )≤1,
)≤1,
则△ABC周长的取值范围是(3+ ,3
,3 ].
].
考点:1.正弦定理;2.三角恒等变换;3.三角函数的图像与性质.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源:2015届北京市西城区高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知函数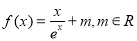 。
。
(1)当 时,求
时,求 的单调区间、最大值;
的单调区间、最大值;
(2)设函数 ,若存在实数
,若存在实数 使得
使得 ,求m的取值范围。
,求m的取值范围。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高二10月月考数学试卷(解析版) 题型:选择题
设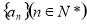 是各项为正数的等比数列,
是各项为正数的等比数列,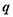 是其公比,
是其公比,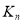 是其前
是其前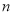 项的积,且
项的积,且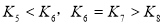 ,则下列结论错误的是( )
,则下列结论错误的是( )
A、 B、
B、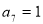
C、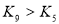 D、
D、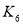 与
与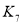 均为
均为 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高二10月月考数学试卷(解析版) 题型:选择题
在等差数列 中,
中, =
= ,则数列
,则数列 的前11项和
的前11项和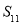 =( ).
=( ).
A.24 B.48 C.66 D.132
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高二上学期期中考试文科数学试卷(解析版) 题型:填空题
下列4个命题:
①“如果 ,则
,则 、
、 互为相反数”的逆命题
互为相反数”的逆命题
②“如果 ,则
,则 ”的否命题
”的否命题
③在 中,“
中,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
④“函数 为奇函数”的充要条件是“
为奇函数”的充要条件是“ ”
”
其中真命题的序号是_________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
若 为实数,则下列命题正确的是( )
为实数,则下列命题正确的是( )
A.若 ,则
,则
B.若 ,则
,则
C.若 ,则
,则
D.若 ,则
,则
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省高一上学期第一次质检数学试卷(解析版) 题型:选择题
(10分)已知全集U为R,集合A={x|0<x≤2},B={x|x<-3或x>1}.
求:(1)A∩B; (2)(∁UA)∩(∁UB); (3)∁U(A∪B).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com