练习册

  • 练习册
  • 试题
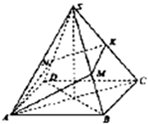
    精英家教网 > 高中数学 > 题目详情
    精英家教网如图，设S-ABCD是一个高为3的四棱锥，底面ABCD的边长为2的正方形，顶点S在底面上的射影是正方形ABCD的中心，K是棱SC的中点，过AK作平面与线段SB，SD分别交于M，N（M，N可以是线段的端点）．
    （1）求直线AK平面SBC所成角的正弦值；
    （2）当M是SB中点时，求四棱锥 S-AMKN 的体积．
    分析：（1）设AK与平面SBC所成角为θ，由SC=
    		32+(
    		2
    )2
    =
    		11
    ，知CK=
    		11
    2
    ，故cos∠SCA=
    		2
    		11
    =
    		22
    11
    ，由此能够求出直线AK平面SBC所成角的正弦值．
    （2）当M是SB的中点时，MK∥BC，由BC∥平面SAD，知MK∥平面SAD，MK∥AN，MK∥AD，故N，D两点重合，由此能求出M是SB中点时，四棱锥 S-AMKN 的体积．
    解答：解：（1）设AK与平面SBC所成角为θ，
    ∵SC=
    		32+(
    		2
    )2
    =
    		11
    ，∴CK=
    		11
    2
    ．
    ∴cos∠SCA=
    		2
    		11
    =
    		22
    11
    ，
    ∴AK2=AC2+CK2-2AC•CK•cos∠SCA=
    27
    4
    ．
    ∴AK=
    3
    		3
    2
    ．
    ∵VS-ABC=
    1
    3
    ×
    1
    2
    ×2×2×3    =2=VA-BCS，
    ∴h=
    6
    S△SBC
    =
    3
    		10
    5
    ，
    ∴sinθ=
    h
    AK
    =
    2
    		30
    15
    ．
    精英家教网
    （2）当M是SB的中点时，MK∥BC，
    ∵BC∥平面SAD，∴MK∥平面SAD，
    ∴MK∥AN，MK∥AD，
    ∴N，D两点重合，
    ∴M到平面SAK的距离为
    		2
    2
    ，
    ∴S△SAK=
    1
    2
    S△SAC=
    3
    		2
    2
    ，
    ∴M是SB中点时，四棱锥 S-AMKN 的体积：
    VS-AMKN=
    1
    3
    ×S△SAK•
    		2
    +
    1
    3
    ×S△SAC•
    		2
    2
    =
    		2
    2
    •S△SAK    =
    		2
    2
    ×
    3
    		2
    2
    =
    3
    2
    ．
    点评：本题考查直线与平面所成角的正弦值的求法，考查四棱锥的体积的求法．解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，在四边形ABCD中，AD=8，CD=6，AB=13，∠ADC=90°且
    AB
    •
    AC
    =50    ．
    （I）求sin∠BAD的值；
    （II）设△ABD的面积为S△ABD，△BCD的面积为S△BCD，求
    S△ABD
    S△BCD
    的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：阅读理解

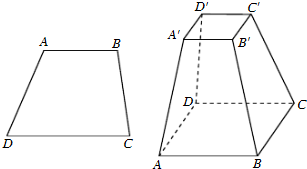    （必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
    方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
    设OE=x，∵△OAB∽△ODC，∴
    x
    x+h
    =
    a
    b
    ，即x=
    ah
    b-a
    ．
    ∴S梯形ABCD=S△ODC-S△OAB=
    1
    2
    b（x+h）-
    1
    2
    ax=
    1
    2
    （b-a）x+
    1
    2
    bh=
    1
    2
    （a+b）h．
    方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
    设梯形AMNB的高为x，MN=y，
    x
    h
    =
    y-a
    b-a
    ⇒y=a+
    b-a
    h
    x，∴S梯形ABCD=
    ∫
    h
    0
    （a+
    b-a
    h
    x）dx=（ax+
    b-a
    2h
    x2）
    |
    h
    0
    =ah+
    b-a
    2h
    •h2=
    1
    2
    （a+b）h．
    再解下面的问题：
    已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S1，S2（S1＜S2），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=
    1
    3
    ×底面积×高）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

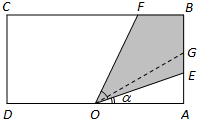    精英家教网如图一块长方形区域ABCD，AD=2（km），AB=1（km）．在边AD的中点O处，有一个可转动的探照灯，其照射角∠EOF始终为
    π
    4
    ，设∠AOE=α，探照灯O照射在长方形ABCD内部区域的面积为S．
    （1）当0≤α＜
    π
    2
    时，写出S关于α的函数表达式；
    （2）若探照灯每9分钟旋转“一个来回”（OE自OA转到OC，再回到OA，称“一个来回”，忽略OE在OA及OC反向旋转时所用时间），且转动的角速度大小一定，设AB边上有一点G，且∠AOG=
    π
    6
    ，求点G在“一个来回”中，被照到的时间．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖南省高一上学期第三次阶段性测试数学卷 题型：解答题

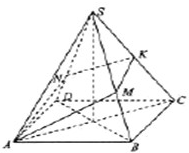
    如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=

    (1)求证:BC⊥SC; (2)设棱SA的中点为M,求证：DM⊥SB.

     

    查看答案和解析>>

    同步练习册答案