
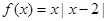
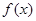 的单调区间
的单调区间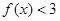
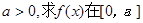 上的最大值
上的最大值科目:高中数学 来源:不详 题型:解答题
 ,上、下两边各空2
,上、下两边各空2 ,左、右两边各空1
,左、右两边各空1 .你如何设计海报的尺寸,才能使四周空白面积最小?
.你如何设计海报的尺寸,才能使四周空白面积最小?
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
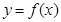 在
在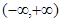 内有定义.对于给定的正数
内有定义.对于给定的正数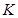 ,定义函数
,定义函数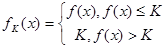 , 取函数
, 取函数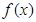 =
=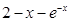 .若对任意的
.若对任意的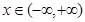 ,恒有
,恒有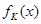 =
=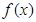 ,则 ( )
,则 ( ) A.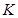 的最小值为1 的最小值为1 | B.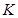 的最大值为2 的最大值为2 | C.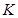 的最大值为1 的最大值为1 | D.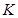 的最小值为2 的最小值为2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 吨,应交水费
吨,应交水费 元。
元。 关于
关于 的函数关系;
的函数关系; ,共交水费26.4元,分别求出甲、乙两用户该月的用水量和水费。
,共交水费26.4元,分别求出甲、乙两用户该月的用水量和水费。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
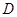 内的任意一个自变量
内的任意一个自变量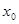 ,都有函数值
,都有函数值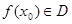 ,则称函数
,则称函数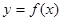 在
在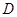 上封闭。若定义域
上封闭。若定义域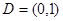 ,则函数①
,则函数①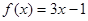 ;②
;②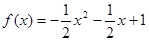 ;③
;③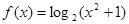 ;④
;④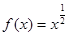 ,其中在
,其中在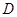 上封闭的是 .
上封闭的是 . 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com