
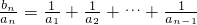 (n≥2且n∈N*).
(n≥2且n∈N*).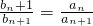 (n≥2);
(n≥2);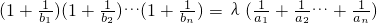 (n∈N*),求实数λ的值.
(n∈N*),求实数λ的值. =
= +
+ +…+
+…+ (n≥2且n∈N*),
(n≥2且n∈N*),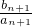 =
= +
+ +…+
+…+ +
+ ,
,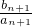 =
= +
+ ,
,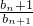 =
=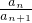 (n≥2且n∈N*). (7分)
(n≥2且n∈N*). (7分)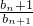 =
=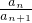 ,b2=a2,
,b2=a2,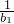 )(1+
)(1+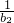 )…(1+
)…(1+ )=
)=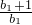 •
•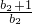 …
…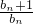 =
=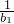 •
•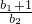 •
• …
…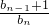 •
•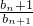 •bn+1
•bn+1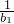 •
•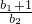 •
•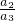 •
•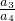 …
…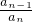 •
•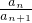 •bn+1
•bn+1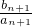
 +
+ +…+
+…+ +
+ ),
),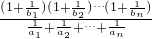 =2,即 λ=2. (14分)
=2,即 λ=2. (14分) =
= +
+ +…+
+…+ (n≥2且n∈N*),向上类比一项,整理即可证得结论;
(n≥2且n∈N*),向上类比一项,整理即可证得结论;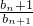 =
=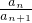 知,(1+
知,(1+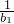 )(1+
)(1+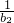 )…(1+
)…(1+ )=2•
)=2•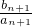 ,而
,而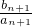 =
= +
+ +…+
+…+ +
+ ,从而可求得
,从而可求得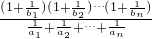 =2,即λ可求.
=2,即λ可求.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| bn |
| an |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an-1 |
| bn+1 |
| bn+1 |
| an |
| an+1 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省吉安市高二(下)期末数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2013年上海市闸北区高考数学二模试卷(理科)(解析版) 题型:解答题
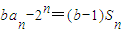 ,
,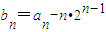 .其中Sn为数列{an}的前n项和.
.其中Sn为数列{an}的前n项和.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com