
分析 根据极值的意义可知,极值点x1、x2是导函数d的零点,根据根的分布建立不等关系,画出满足条件的区域,明确目标函数的几何意义,即可求得结论.
解答 解:f′(x)=x2+2ax+2b=g(x),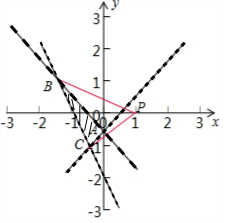
∵函数f(x)=$\frac{1}{3}$x3+ax2+2bx+c有两个极值点x1,x2,
且-1<x1<1<x2<2,
则x1,x2是函数g(x)的两个零点,
∴$\left\{\begin{array}{l}{△=4{a}^{2}-8b>0}\\{g(-1)=1-2a+2b>0}\\{g(1)=1+2a+2b<0}\\{g(2)=4+4a+2b>0}\end{array}\right.$,其中△>0可以去掉.
画出可行域:平面三角形ABC的内部的所有点.
A$(0,-\frac{1}{2})$,B$(-\frac{3}{2},1)$,C$(-\frac{1}{2},-1)$.
直线bx-(a-1)y+3=0的斜率k=$\frac{b}{a-1}$,表示经过两点(a,b),P(1,0)的直线的斜率.
kPC=$\frac{1}{1+\frac{1}{2}}$=$\frac{2}{3}$,kPB=$\frac{1}{-\frac{3}{2}-1}$=-$\frac{2}{5}$.
∴$-\frac{2}{5}<k<\frac{2}{3}$.
故答案为:$(-\frac{2}{5},\frac{2}{3})$.
点评 本题考查了利用导数研究函数的单调性极值、解不等式、线性规划、二次函数的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我们通常把圆、椭圆、抛物线、双曲线统称为圆锥曲线.通过普通高中课程实验教科书《数学》2-1第二章《圆锥曲线与方程》章头引言我们知道,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.实际上,设圆锥母线与轴所成角为α,不过圆锥顶点的截面与轴所成角为θ.当θ=$\frac{π}{2}$,截口曲线为圆,当$α<θ<\frac{π}{2}$时,截口曲线为椭圆;当0≤θ<α时,截口曲线为双曲线; 当θ=α时,截口曲线为抛物线;如图2,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
我们通常把圆、椭圆、抛物线、双曲线统称为圆锥曲线.通过普通高中课程实验教科书《数学》2-1第二章《圆锥曲线与方程》章头引言我们知道,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.实际上,设圆锥母线与轴所成角为α,不过圆锥顶点的截面与轴所成角为θ.当θ=$\frac{π}{2}$,截口曲线为圆,当$α<θ<\frac{π}{2}$时,截口曲线为椭圆;当0≤θ<α时,截口曲线为双曲线; 当θ=α时,截口曲线为抛物线;如图2,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )| A. | 一段双曲线弧 | B. | 一段椭圆弧 | C. | 一段圆弧 | D. | 一段抛物线弧 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:解答题
已知定义域为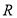 的函数
的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)用定义证明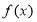 在
在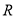 上是单调递减函数;
上是单调递减函数;
(3)若对任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com