
分析 (Ⅰ)利用已知条件列出椭圆几何量的方程组,求解a,b,即可求椭圆C的方程;
(Ⅱ)联立直线与椭圆方程,利用韦达定理,结合向量关系,推出结果即可.
解答 解:( I)由已知可$\left\{{\begin{array}{l}{2c=2}\\{\frac{c}{a}=\frac{{\sqrt{2}}}{2}}\end{array}}\right.$解得$\left\{{\begin{array}{l}{a=\sqrt{2}}\\{c=1}\end{array}}\right.$,∴b=1.
所求椭圆C的方程$\frac{x^2}{2}+{y^2}=1$. …(4分)
( II)由$\left\{{\begin{array}{l}{y=kx+m}\\{{x^2}+2{y^2}=2}\end{array}}\right.$得(1+2k2)x2+4kmx+2m2-2=0,
∴△=16k2m2-4(1+2k2)(2m2-2)=8(1+2k2-m2).
由直线直线l与椭圆C交于不同的A,B两点,有△>0,∴1+2k2>m2. ①
设点A(x1,y1),B(x2,y2),则$\left\{{\begin{array}{l}{{x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}}}\\{x{\;}_1{x_2}=\frac{{2{m^2}-2}}{{1+2{k^2}}}}\end{array}}\right.$
于是${y_1}+{y_2}=k({x_1}+{x_2})+2m=\frac{2m}{{1+2{k^2}}}$. …(8分)
当m=0时,易知点A,B关于原点对称,则λ=0;
当m≠0时,易知点A,B不关于原点对称,则λ≠0.
由$\overrightarrow{OA}+\overrightarrow{OB}=λ\overrightarrow{OQ}$,得$\left\{{\begin{array}{l}{{x_Q}=\frac{1}{λ}({x_1}+{x_2})}\\{{y_Q}=\frac{1}{λ}({y_1}+{y_2})}\end{array}}\right.$即$\left\{{\begin{array}{l}{{x_Q}=\frac{-4km}{{λ(1+2{k^2})}}}\\{{y_Q}=\frac{2m}{{λ(1+2{k^2})}}}\end{array}}\right.$.
∵Q点在椭圆上,∴${[\frac{-4km}{{λ(1+2{k^2})}}]^2}+2{[\frac{2m}{{λ(1+2{k^2})}}]^2}=2$.
化简得4m2(1+2k2)=λ2(1+2k2)2.
∵1+2k2≠0,∴4m2=λ2(1+2k2). ②
由①②两式可得λ2<4,∴-2<λ<2且λ≠0.
综上可得实数λ的取值范围是-2<λ<2. …(14分)
点评 本题考查椭圆方程的求法,椭圆的简单性质以及圆锥曲线的范围问题的解法,考查分析问题解决问题以及转化思想的应用.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:选择题
下列结论判断正确的是( )
A.任意两条直线确定一个平面
B.三条平行直线最多确定三个平面
C.棱长为1的正方体的内切球的表面积为
D.若平面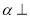 平面
平面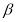 ,平面
,平面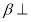 平面
平面 ,则平面
,则平面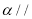 平面
平面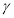
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:选择题
若不等式 表示的平面区域为
表示的平面区域为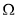 ,
,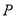 、
、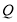 均为
均为 内一点,
内一点, 为坐标原点,
为坐标原点, ,则下列判断正确的是( )
,则下列判断正确的是( )
A.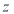 的最小值为
的最小值为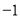 B.
B. 的最小值为
的最小值为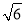
C. 的最大值为
的最大值为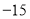 D.
D.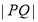 的最大值为
的最大值为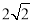
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
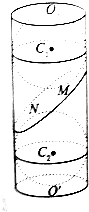 如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )
如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )| A. | 7500π | B. | 7200π | C. | 7800π | D. | 8100π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{14}}}{6}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com