
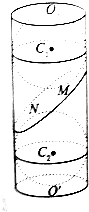
 如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )
如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )| A. | 7500π | B. | 7200π | C. | 7800π | D. | 8100π |
分析 根据地面半径和截面与底面的夹角计算椭圆的长短轴,从而求出圆柱的高,代入圆柱的体积公式即可得出.
解答  解:设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
解:设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
设椭圆的长轴一端点为A,球C2与A所在的母线的切点为B,C2N,C2A,C2B,
则$\left\{\begin{array}{l}{2acosβ=24}\\{2b=24}\end{array}\right.$,∴a=13,b=12,∴c=$\sqrt{{a}^{2}-{b}^{2}}$=5,
∴AN=a-c=8.
∵Rt△ANC2∽Rt△ABC2,
∴AB=AN=8,
∴圆柱的高OO′=2×(12+8)+2asinβ=50.
∴圆柱的体积V=π×122×50=7200π.
故选B.
点评 本题考查了圆柱的体积计算,计算椭圆的长短轴是解题关键.


科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(理)试卷(解析版) 题型:解答题
已知函数 在
在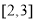 上有最小值1和最大值4,设
上有最小值1和最大值4,设 .
.
(1)求 的值;
的值;
(2)若不等式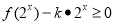 在
在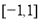 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:解答题
如图,在三棱柱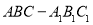 中,
中,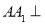 平面
平面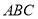 ,
, ,
,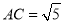 ,
,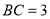 ,
, ,
, 分别为
分别为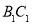 、
、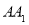 的中点.
的中点.
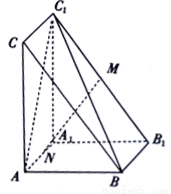
(1)求证:平面 平面
平面 ;
;
(2)求证: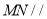 平面
平面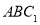 ,并求
,并求 到平面
到平面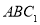 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:选择题
为了了解某学校1200名高中男生的身体发育情况,抽查了该校100名高中男生的体重情况.根据所得数据画出样本的频率分布直方图,据此估计该校高中男生体重在 的人数为( )
的人数为( )
A.360 B.336 C.300 D.280

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:解答题
已知定义域为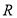 的函数
的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)用定义证明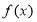 在
在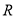 上是单调递减函数;
上是单调递减函数;
(3)若对任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | 4 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com