
为了了解某学校1200名高中男生的身体发育情况,抽查了该校100名高中男生的体重情况.根据所得数据画出样本的频率分布直方图,据此估计该校高中男生体重在 的人数为( )
的人数为( )
A.360 B.336 C.300 D.280

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:选择题
已知定义在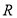 上的函数
上的函数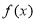 满足:
满足: 的图象关于
的图象关于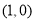 点对称,且当
点对称,且当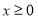 时恒有
时恒有 ,当
,当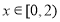 时,
时,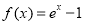 ,则
,则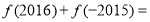 ( )
( )
A.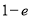 B.
B.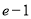
C.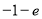 D.
D.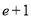
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:选择题
若不等式 表示的平面区域为
表示的平面区域为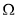 ,
,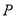 、
、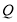 均为
均为 内一点,
内一点, 为坐标原点,
为坐标原点, ,则下列判断正确的是( )
,则下列判断正确的是( )
A.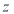 的最小值为
的最小值为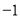 B.
B. 的最小值为
的最小值为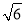
C. 的最大值为
的最大值为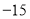 D.
D.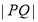 的最大值为
的最大值为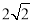
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
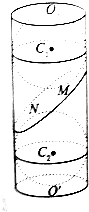 如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )
如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )| A. | 7500π | B. | 7200π | C. | 7800π | D. | 8100π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com