
���� ��1������y=��sin�ȣ�x=��cos�ȣ���C�ļ����귽�̻���ֱ�����귽�̣��ɵ�ԲC��Բ�ĵļ����ꣻ
��2�����P��ֱ��AB��������ֵ��|AB|��������������PAB��������ֵ��
��� �⣺��1��ԲC�ļ����귽���Ǧ�=2$\sqrt{2}$cos����+$\frac{��}{4}$������Ϊ��=2cos��-2sin�ȣ�
���2=2��cos��-2��sin�ȣ�
�ɦ�cos��=x����sin��=y����x2+y2-2x+2y=0������x-1��2+��y+1��2=2��
��Բ������Ϊ��1��-1����������Ϊ��$\sqrt{2}$��$\frac{7��}{4}$����
��2��ֱ�ߵ���ͨ����Ϊ2$\sqrt{2}$x-y-1=0��
Բ�ĵ�ֱ��l�ľ���Ϊd=$\frac{|2\sqrt{2}+1-1|}{3}$=$\frac{2\sqrt{2}}{3}$��
���ҳ�|AB|=2$\sqrt{2-\frac{8}{9}}$=$\frac{2\sqrt{10}}{3}$��
��P��ֱ��AB��������ֵΪ$\sqrt{2}$+$\frac{2\sqrt{2}}{3}$=$\frac{5\sqrt{2}}{3}$��
��������PAB��������ֵΪ$\frac{1}{2}��\frac{2\sqrt{10}}{3}��\frac{5\sqrt{2}}{3}=\frac{10\sqrt{5}}{9}$��
���� �������е��⣬���鼫���귽����ֱ�����귽�̵Ļ������㵽ֱ�ߵľ��빫ʽ��Ӧ�ã��������������


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�������ѧ�߶����¿�һ��ѧ�������Ծ��������棩 ���ͣ�ѡ����
Ϊ���˽�ijѧУ1200���������������巢�����������˸�У100��������������������������������ݻ���������Ƶ�ʷֲ�ֱ��ͼ���ݴ˹��Ƹ�У�������������� ������Ϊ�� ��
�������� ��
A��360 B��336 C��300 D��280

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�갲������һ�и�һ�Ϲ�����ҵ����ѧ�Ծ��������棩 ���ͣ������
��֪������Ϊ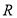 �ĺ���
�ĺ��� ���溯��.
���溯��.
��1���� ��ֵ��
��ֵ��
��2���ö���֤��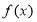 ��
��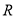 ���ǵ����ݼ�������
���ǵ����ݼ�������
��3���������� ������ʽ
������ʽ ���������
��������� ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
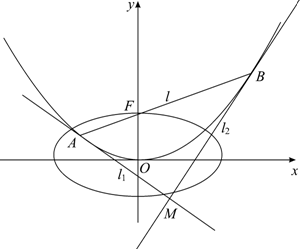 ��֪������C��x2=4y�Ľ���ΪF������F��ֱ��l��������C��A��B���㣻��ԲE��������ԭ�㣬������x���ϣ���F������һ�����㣬����������e=$\frac{{\sqrt{3}}}{2}$��
��֪������C��x2=4y�Ľ���ΪF������F��ֱ��l��������C��A��B���㣻��ԲE��������ԭ�㣬������x���ϣ���F������һ�����㣬����������e=$\frac{{\sqrt{3}}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | 1 | C�� | 4 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{3}{8}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{5}{8}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com