
分析 先求出基本事件总数N=4×4=16,再求出幂函数f(x)=(m-n)2x${\;}^{\frac{m}{n}}$图象关于y轴对称满足条件的基本事件的个数,由此能求出使得幂函数f(x)=(m-n)2x${\;}^{\frac{m}{n}}$图象关于y轴对称的概率.
解答 解:箱子里装有4张大小、形状都相同的卡片,标号分别为1,2,3,4.
从箱子中任意取出一张卡片,记下它的标号m,然后再放回箱子中;
第二次再从箱子中任取一张卡片,记下它的标号n,
则基本事件总数N=4×4=16,
∵幂函数f(x)=(m-n)2x${\;}^{\frac{m}{n}}$图象关于y轴对称,
∴$\left\{\begin{array}{l}{m-n=±1}\\{m}是偶数}\end{array}\right.$,满足条件的基本事件有:(2,1),(2,3),(4,3),共3种,
使得幂函数f(x)=(m-n)2x${\;}^{\frac{m}{n}}$图象关于y轴对称的概率为$\frac{3}{16}$.
故答案为:$\frac{3}{16}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
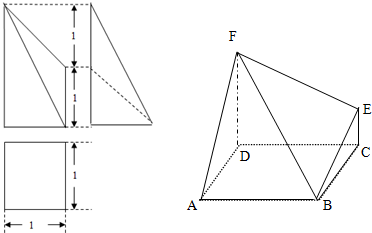
 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
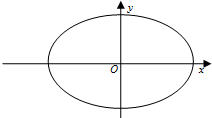 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,左、右焦点分别是F1、F2,以原点O为圆心,椭圆C的短半轴为半径的圆与直线l:x-y+2=0相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,左、右焦点分别是F1、F2,以原点O为圆心,椭圆C的短半轴为半径的圆与直线l:x-y+2=0相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com