
分析 根据题意画出直线与圆的图形,结合图形求出对应图形的面积比即可.
解答 解:圆(x-1)2+(y+3)2=36的圆心为(1,-3),半径为6,
它的面积为π×62=36π,
画出直线3x-4y=0与圆的图形,如图所示;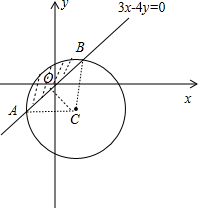
根据几何图形得出:AC=6,
圆心C到直线3x-4y=0的距离为:
d=$\frac{|3×1-4×(-3)|}{\sqrt{{3}^{2}{+(-4)}^{2}}}$=3,
∴∠APB=30°,
∴∠ACB=120°;
∴阴影部分的面积为:
S阴影=$\frac{1}{3}$π×62-$\frac{1}{2}$×62×sin120°=12π-9$\sqrt{3}$;
∴所求的概率为:
P=$\frac{{S}_{阴影}}{{S}_{圆}}$=$\frac{12π-9\sqrt{3}}{36π}$=$\frac{1}{3}$-$\frac{\sqrt{3}}{4π}$.
故答案为:$\frac{1}{3}$-$\frac{\sqrt{3}}{4π}$.
点评 本题主要考查了几何概型的概率计算问题,根据条件求出对应图形的面积是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:解答题
已知定义域为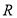 的函数
的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)用定义证明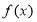 在
在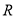 上是单调递减函数;
上是单调递减函数;
(3)若对任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
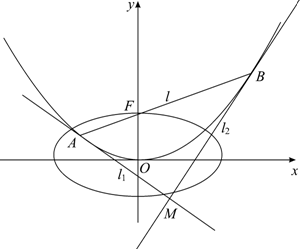 已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=$\frac{{\sqrt{3}}}{2}$.
已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com