
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:解答题
已知 为等比数列
为等比数列 的前
的前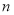 项和,
项和,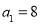 ,且
,且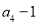 ,
,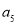 ,
, 成等差数列.
成等差数列.
(1)求数列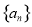 的通项公式及
的通项公式及 ;
;
(2)若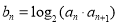 ,
,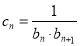 ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com