
分析 (1)利用函数y=f(x)-2为奇函数得到b,讨论a,利用其单调性和基本不等式得到求出a值,进而得到f(x);
(2)把a=1代入f(x)=$\frac{1}{x}$+ax+b,由题意可得-2b=$\frac{2}{x}$+x,令h(x)=$\frac{2}{x}$+x,求出单调区间和端点的函数值,即可得到b的范围和最小值;
(3)由f(x)=$\frac{1}{x}$+ax+b,得f′(x)=-$\frac{1}{{x}^{2}}$+a=$\frac{a{x}^{2}-1}{{x}^{2}}$,判断函数f(x)的单调性,由题意,讨论得到a的范围.
解答 解:(1)由题意得,函数y=f(x)-2=$\frac{1}{x}$+ax+b-2,
令y=g(x)=f(x)-2为奇函数,∴g(-x)=-g(x),
即-$\frac{1}{x}$-ax+b-2=-($\frac{1}{x}$+ax+b-2),解得b=2,
由y=$\frac{1}{x}$+ax在(0,+∞)上的最小值为4,
当a≤0时,函数递减无最小值;
当a>0时,y=$\frac{1}{x}$+ax≥2$\sqrt{ax•\frac{1}{x}}$,
即有ax=$\frac{1}{x}$时取得最小值2$\sqrt{a}$=4,
解得a=4,则f(x)=$\frac{1}{x}$+4x+2;
(2)把a=1代入得f(x)=$\frac{1}{x}$+x+b,
则g(x)=$\frac{2}{x}$+x+2b在[$\frac{1}{2}$,2]上有两个不同的零点,
即有-2b=$\frac{2}{x}$+x,令h(x)=$\frac{2}{x}$+x,则h(x)在[$\frac{1}{2}$,$\sqrt{2}$)递减,在($\sqrt{2}$,2]递增,
可得h($\sqrt{2}$)=2$\sqrt{2}$,h($\frac{1}{2}$)=$\frac{9}{2}$,h(2)=3,
由g(x)=$\frac{2}{x}$+x+2b在[$\frac{1}{2}$,2]上有两个不同的零点,
可得2$\sqrt{2}$<-2b≤$\frac{9}{2}$,
解得-$\frac{9}{4}$≤b<-$\sqrt{2}$,
即b的最小值为-$\frac{9}{4}$;
(3)由f(x)=$\frac{1}{x}$+ax+b,得f′(x)=-$\frac{1}{{x}^{2}}$+a=$\frac{a{x}^{2}-1}{{x}^{2}}$,
由f′(x)≤0,得a≤$\frac{1}{{x}^{2}}$,所以a≤$\frac{1}{4}$,此时f(x)在区间[$\frac{1}{2}$,2]上为减函数,
要使对任意的实数b,都存在实数x0∈[$\frac{1}{2}$,2],使得不等式|f(x0)|≥$\frac{1}{2}$成立,
只要f(x0)≥$\frac{1}{2}$或者f(x0)≤-$\frac{1}{2}$所以只要f(x)的最大值为f($\frac{1}{2}$)=2+$\frac{1}{2}$a+b≥$\frac{1}{2}$
或者f(2)=$\frac{1}{2}$+2a+b≤-$\frac{1}{2}$.
解得a≤$\frac{1}{3}$,又a≤$\frac{1}{4}$,
所以a≤$\frac{1}{4}$;
由f′(x)≥0,由x∈[$\frac{1}{2}$,2],得a≥$\frac{1}{{x}^{2}}$,得到a≥4,此时f(x)在区间[$\frac{1}{2}$,2]上为增函数,
要使对任意的实数b,都存在实数x0∈[$\frac{1}{2}$,2],使得不等式|f(x0)|≥$\frac{1}{2}$成立,
只要f(x0)≥$\frac{1}{2}$或者f(x0)≤-$\frac{1}{2}$所以只要f(x)的最大值为f(2)=$\frac{1}{2}$+2a+b≥$\frac{1}{2}$
或者f($\frac{1}{2}$)=2+$\frac{1}{2}$a+b≤-$\frac{1}{2}$.
解得a≥$\frac{5}{3}$,又a≥4,
所以a≥4;
综上a≥4或a≤$\frac{1}{4}$.
点评 本题考查函数的单调性,最值与导数的关系,和存在性问题的转化,属于压轴题,难题.


科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
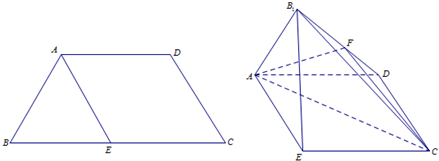
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com