
科目:高中数学 来源: 题型:
某市文化馆在春节期间举行高中生“蓝天海洋杯”象棋比赛,规则如下:两名选手比赛时,每局胜者得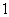 分,负者得
分,负者得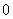 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多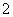 分或打满
分或打满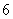 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为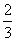 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响.
(Ⅰ)求比赛进行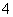 局结束,且乙比甲多得
局结束,且乙比甲多得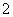 分的概率;
分的概率;
(Ⅱ)设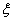 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量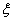 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
设点 到直线
到直线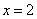 的距离与它到定点
的距离与它到定点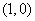 的距离之比为
的距离之比为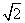 ,并记点
,并记点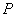 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设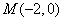 ,过点
,过点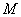 的直线
的直线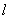 与曲线
与曲线 相交于
相交于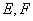 两点,当线段
两点,当线段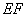 的中点落在由四点
的中点落在由四点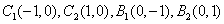 构成的四边形内(包括边界)时,求直线
构成的四边形内(包括边界)时,求直线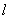 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com