
、(12分)设函数f(x) = x2+bln(x+1),
(1)若对定义域的任意x,都有f(x)≥f(1)成立,求实数b的值;
(2)若函数f(x)在定义域上是单调函数,求实数b的取值范围;
(3)若b=-1,证明对任意的正整数n,不等式 成立;
成立;
(1) b= - 4
(2) 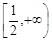
(3)略
【解析】解:(1)由x + 1>0得x> – 1∴f(x)的定义域为( - 1,+ ∞),
对x∈ ( - 1,+ ∞),都有f(x)≥f(1),∴f(1)是函数f(x)的最小值,故有f/ (1) = 0,
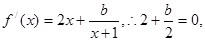 解得b= - 4.…………………………2分
解得b= - 4.…………………………2分
经检验,列表(略),合题意;……………………4分
(2)∵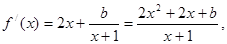 又函数f(x)在定义域上是单调函数,
又函数f(x)在定义域上是单调函数,
∴f/ (x) ≥0或f/(x)≤0在( - 1,+ ∞)上恒成立。
若f/ (x) ≥0,∵x + 1>0,∴2x2 +2x+b≥0在( - 1,+ ∞)上恒成立,
即b≥-2x2 -2x = 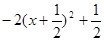 恒成立,由此得b≥
恒成立,由此得b≥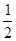 ;
;
若f/ (x) ≤0, ∵x + 1>0, ∴2x2 +2x+b≤0,即b≤- (2x2+2x)恒成立,
因-(2x2+2x) 在( - 1,+ ∞)上没有最小值,∴不存在实数b使f(x) ≤0恒成立。
综上所述,实数b的取值范围是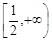 。………………………………8分
。………………………………8分
(3)当b= - 1时,函数f(x) = x2 - ln(x+1),
令函数h(x)=f(x) – x3 = x2 – ln(x+1) – x3,
则h/(x) = - 3x2 +2x - 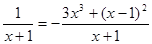 ,
,
∴当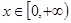 时,h/(x)<0所以函数h(x)在
时,h/(x)<0所以函数h(x)在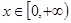 上是单调递减。
上是单调递减。
又h(0)=0,∴当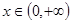 时,恒有h(x) <h(0)=0,
时,恒有h(x) <h(0)=0,
即x2 – ln(x+1) <x3恒成立.故当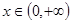 时,有f(x)
<x3..
时,有f(x)
<x3..
∵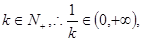 取
取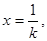 则有
则有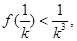
∴ ,故结论成立。……………………12分
,故结论成立。……………………12分


科目:高中数学 来源: 题型:
设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值.
(1)求a、b的值;
(2)若对任意的x∈[0,3],都有f(x)<c2成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=![]() x-lnx(x>0),则y=f(x) ( )
x-lnx(x>0),则y=f(x) ( )
A.在区间(![]() ,1),(1,e)内均有零点
,1),(1,e)内均有零点
B.在区间(![]() ,1),(1,e)内均无零点
,1),(1,e)内均无零点
C.在区间(![]() ,1)内有零点,在区间(1,e)内无零点
,1)内有零点,在区间(1,e)内无零点
D.在区间(![]() ,1)内无零点,在区间(1,e)内有零点
,1)内无零点,在区间(1,e)内有零点
查看答案和解析>>
科目:高中数学 来源:2014届湖北武汉部分重点中学高二下学期期中考试理数学试卷(解析版) 题型:解答题
已知实数a满足1<a≤2,设函数f (x)= x3-
x3- x2+a x.
x2+a x.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于或等于10.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省高三第三次月考数学文卷 题型:解答题
设函数f(x)= -6x+5,X
-6x+5,X R
R
(1) 求函数f(x)的单调区间和极值
(2) 若关于x的方程f(x)=a有三个不同实根,求实数a的范围.
(3) 已知当x (1,+∞)时,f(x)≥K(x-1)恒成立,求实数K的取值范围。
(1,+∞)时,f(x)≥K(x-1)恒成立,求实数K的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com