
设函数f(x)= -6x+5,X
-6x+5,X R
R
(1) 求函数f(x)的单调区间和极值
(2) 若关于x的方程f(x)=a有三个不同实根,求实数a的范围.
(3) 已知当x (1,+∞)时,f(x)≥K(x-1)恒成立,求实数K的取值范围。
(1,+∞)时,f(x)≥K(x-1)恒成立,求实数K的取值范围。
(1) f(x)的单调增区间为(-∞,- )和(
)和( ,∞)
,∞)
f(x)的单调减区间为〔- ,
, 〕
〕
(2) 5-4 ≤a<5+4
≤a<5+4 时
时
(3) K≤-3
【解析】(1)∵f(x′)=3X2-6=0, x1=- , x2=
, x2=
∴当x<- 或x>
或x> 时,f(x′)>0,当-
时,f(x′)>0,当- <x<
<x< 时,f(x′)<0
时,f(x′)<0
∴f(x)的单调增区间为(-∞,- )和(
)和( ,∞)
,∞)
f(x)的单调减区间为〔- ,
, 〕
(4分)
〕
(4分)
当x=- 时,f(x)有极大值5+4
时,f(x)有极大值5+4 ,当x=
,当x= 时,f(x)有极小值5-4
时,f(x)有极小值5-4
(2)由(1)知当5-4 ≤a<5+4
≤a<5+4 时,直线y=a与Y=f(x)的图象有三个不同的交点,
时,直线y=a与Y=f(x)的图象有三个不同的交点,
即方程f(x)=a有三个不同解 (8分)
(3)f(x)≥K(x-1)即(x-1)(x2+x-5)≥K(x-1)
∵K>1 ∴K≤(x2+x-5)在(1,+∞)上恒成立
g(x)=(x2+x-5), g(x)在(1,+∞)增函数
∴g(x)>g(1)=-3 ∴K的取值范围K≤-3 (12分)


科目:高中数学 来源:2014届湖北武汉部分重点中学高二下学期期中考试理数学试卷(解析版) 题型:解答题
已知实数a满足1<a≤2,设函数f (x)= x3-
x3- x2+a x.
x2+a x.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于或等于10.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年辽宁省高三上学期第三次月考文科数学试卷 题型:解答题
已知实数a满足1<a≤2,设函数f (x)=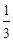 x3-
x3-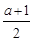 x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三高考样卷数学文卷 题型:解答题
(本题满分15分) 已知实数a满足1<a≤2,设函数f (x)= x3-
x3- x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省高一上学期期末考试数学试卷 题型:选择题
设函数f(x)=2cos2x+ sin2x+a(a为实常数)在区间
sin2x+a(a为实常数)在区间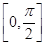 上的最小值为-4,那么a的值等于( )
上的最小值为-4,那么a的值等于( )
A.4 B.-6 C.-3 D.-4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com