
如图1-1-13,已知在梯形ABCD中,AD∥BC,∠ADC=90°,E是AB边的中点,连结ED、EC.求证:ED=EC.
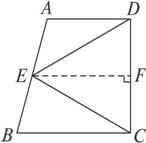
图1-1-13
思路分析:在梯形中,若已知一腰的中点,一般过这点作底边的平行线即可得到另一腰的中点.所以由E是AB边的中点,作EF∥BC交DC于F,即可得EF⊥DC,从而利用线段中垂线的性质得到结论.
证明:过E点作EF∥BC交DC于F.
∵在梯形ABCD中,AD∥BC,∴AD∥EF∥BC.
∵E是AB的中点,∴F是DC的中点(经过梯形一腰的中点与底平行的直线必平分另一腰).
∵∠ADC=90°,∴∠DFE=90°.
∴EF⊥DC于F.又F是DC中点,
∴EF是DC的垂直平分线.
∴ED=EC(线段垂直平分线上的点到线段两端点距离相等).
方法归纳 证明不在同一直线上的两条线段相等,可以根据等腰三角形的两腰相等,或者根据全等三角形对应边相等来证明.


科目:高中数学 来源:广东省惠阳高级中学10-11学年高一下学期期末考试数学 题型:解答题
(本小题满分14分)
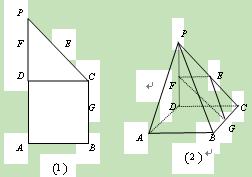
如图(1),在直角梯形 中,
中,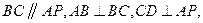
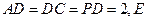 、
、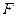 、
、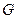 分别是线段
分别是线段 、
、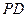 、
、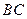 的中点,现将
的中点,现将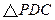 折起,使平面
折起,使平面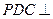 平面
平面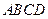 (如图(2)).
(如图(2)).
(Ⅰ)求证: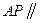 平面
平面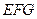 ;
;
(Ⅱ)取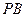 中点为
中点为 ,求证:
,求证: 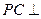 平面
平面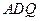 ,
,
查看答案和解析>>
科目:高中数学 来源:2015届广东省高一暑假作业(三)必修2数学试卷(解析版) 题型:解答题
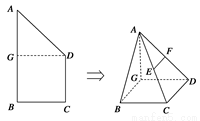
如图,在直角梯形 中,
中,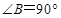 ,
,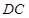 ∥
∥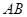 ,
,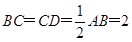 ,
,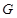 为线段
为线段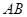 的中点,将
的中点,将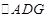 沿
沿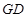 折起,使平面
折起,使平面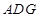 ⊥平面
⊥平面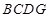 ,得到几何体
,得到几何体 .
.
(1)若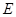 ,
,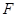 分别为线段
分别为线段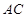 ,
,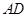 的中点,求证:
的中点,求证: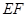 ∥平面
∥平面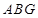 ;
;
(2)求证: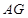 ⊥平面
⊥平面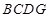 ;
;
(3)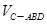 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014届广东省汕头市高二下学期期中文科数学试卷(解析版) 题型:解答题
如图1,在直角梯形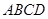 中,
中,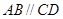 ,
, ,且
,且 .
.
现以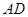 为一边向形外作正方形
为一边向形外作正方形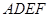 ,然后沿边
,然后沿边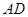 将正方形
将正方形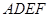 翻折,使平面
翻折,使平面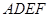 与平面
与平面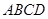 垂直,
垂直, 为
为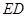 的中点,如图2.
的中点,如图2.
(1)求证: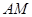 ∥平面
∥平面 ;
;
(2)求证: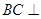 平面
平面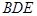 ;
;
(3)求点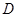 到平面
到平面 的距离.
的距离.
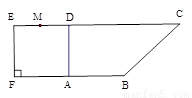

图 图
图
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期期中考试数学试卷 题型:解答题
如图甲,在直角梯形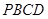 中,
中,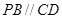 ,
,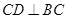 ,
,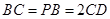 ,
,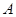 是
是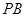 的中点. 现沿
的中点. 现沿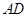 把平面
把平面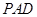 折起,使得
折起,使得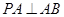 (如图乙所示),
(如图乙所示),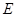 、
、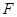 分别为
分别为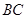 、
、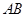 边的中点.
边的中点.
(Ⅰ)求证: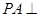 平面
平面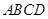 ;
;
(Ⅱ)求证:平面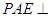 平面
平面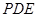 ;
;
(Ⅲ)在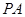 上找一点
上找一点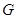 ,使得
,使得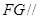 平面
平面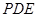 .
.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三5月月考理科数学 题型:解答题
(本题满分14分)
在直角梯形 中,
中,

 将
将
 翻折上去恰好使
翻折上去恰好使

(Ⅰ) 求证: ;
;
(Ⅱ)已知 试求:
试求:
(1) 四面体ABCD内切球的表面积;
(2) 二面角 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com