
| A. | 1 007 | B. | 1 008 | C. | 2 015 | D. | 2 016 |
分析 在f(a+b)=f(a)•f(b)中令b=1得,f(a+1)=f(a)•f(1),变形为$\frac{f(a+1)}{f(a)}$=f(1)=2,可知$\frac{f(2)}{f(1)}$=$\frac{f(4)}{f(3)}$=$\frac{f(6)}{f(5)}$=…=$\frac{f(2016)}{f(2015)}$=2(共有1008项),以此可以答案可求.
解答 解:∵f(x)满足对任意的实数a,b都有f(a+b)=f(a)•f(b),
∴令b=1得,f(a+1)=f(a)•f(1),
∴$\frac{f(a+1)}{f(a)}$=f(1)=2.
∴$\frac{f(2)}{f(1)}$=$\frac{f(4)}{f(3)}$=$\frac{f(6)}{f(5)}$=…=$\frac{f(2016)}{f(2015)}$=2(共有1008项),
∴$\frac{f(2)}{f(1)}$+$\frac{f(4)}{f(3)}$+$\frac{f(6)}{f(5)}$+…+$\frac{f(2016)}{f(2015)}$=1008×2=2016.
故选:D.
点评 本题考查抽象函数值求解,对于抽象函数关键是对字母准确、灵活赋值,构造出更具体的题目需求的关系式,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(2,+∞) | C. | (-2,2) | D. | (-∞,-2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
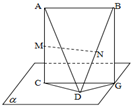 如图,AC⊥平面α于C,BG⊥平面α于G,AB∥平面α,CD?平面α,M、N分别为AC、BD的中点,若AB=4,AC=2,CD=4,BD=6
如图,AC⊥平面α于C,BG⊥平面α于G,AB∥平面α,CD?平面α,M、N分别为AC、BD的中点,若AB=4,AC=2,CD=4,BD=6查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com