
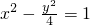 的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部.当(x,y)∈D时,x2+y2+2x的最大值为
的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部.当(x,y)∈D时,x2+y2+2x的最大值为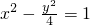 的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部,所以先由题意找到平面区域D,对于x2+y2+2x=z?(x+1)2+y2=z+1此式可以看成圆心为顶点(-1,0),圆的半径随z的变化而变化同心圆系,画出图形求解即可.
的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部,所以先由题意找到平面区域D,对于x2+y2+2x=z?(x+1)2+y2=z+1此式可以看成圆心为顶点(-1,0),圆的半径随z的变化而变化同心圆系,画出图形求解即可.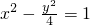 的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部,所以得到区域为:
的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部,所以得到区域为: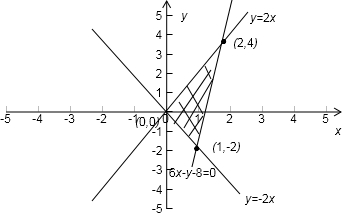


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源:2012-2013学年安徽省高三第七次模拟考试文科数学试卷(解析版) 题型:选择题
设平面区域D是由双曲线 的两条渐近线和直线
的两条渐近线和直线 所围成三角形的边界及内部.当
所围成三角形的边界及内部.当 时,
时, 的最大值为( ).
的最大值为( ).
A.12 B.10 C.8 D.6
查看答案和解析>>
科目:高中数学 来源:2012届云南省高三上期中理科数学试卷(解析版) 题型:选择题
设平面区域D是由双曲线 的两条渐近线和直线
的两条渐近线和直线 所围成三角形的边界及内部。当
所围成三角形的边界及内部。当 时,
时, 的最大值为( )
的最大值为( )
A.8 B.0 C.-2 D.16
查看答案和解析>>
科目:高中数学 来源:2011-2012学年辽宁省、庄河高中高三上学期期末理科数学 题型:选择题
设平面区域D是由双曲线 的两条渐近线和直线
的两条渐近线和直线 所围成三角形的边界及内部.当
所围成三角形的边界及内部.当 时,
时, 的最大值是
的最大值是
A.24 B.25 C.4 D.7
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三下学期3月月考数学理卷 题型:选择题
设平面区域D是由双曲线 的两条渐近线和直线
的两条渐近线和直线 所围成三角形的边界及内部。当
所围成三角形的边界及内部。当 时,
时,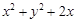 的最大值为( )
的最大值为( )
A.24 B.25 C.4 D.7
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三下学期3月月考数学理卷 题型:选择题
设平面区域D是由双曲线 的两条渐近线和直线
的两条渐近线和直线 所围成三角形的边界及内部。当
所围成三角形的边界及内部。当 时,
时, 的最大值为( )
的最大值为( )
A.24 B.25 C.4 D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com