
设函数f( )=
)= ,且方程
,且方程 的两个根分别为1,4.
的两个根分别为1,4.
(1)当 =3且曲线y=f(x)过原点时,求f(x)的解析式;
=3且曲线y=f(x)过原点时,求f(x)的解析式;
(2)若f(x)在(-∞,+∞)内无极值点,求 的取值范围.
的取值范围.
(1)f(x)=x3-3x2+12x;(2)[1,9]
【解析】
试题分析:(1)方程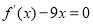 的两个根分别为1,4可知关于a、b、c的两个方程,又a=3,解得b=-3,c=12,而曲线过原点,所以d=0,所以解析式为f(x)=x3-3x2+12x,(2)由于a>0,所以“f(x)=x3+bx2+cx+d在(-∞,+∞)内无极值点”等价于“f′(x)=ax2+2bx+c≥0在(-∞,+∞)内恒成立”,因此a>0,
的两个根分别为1,4可知关于a、b、c的两个方程,又a=3,解得b=-3,c=12,而曲线过原点,所以d=0,所以解析式为f(x)=x3-3x2+12x,(2)由于a>0,所以“f(x)=x3+bx2+cx+d在(-∞,+∞)内无极值点”等价于“f′(x)=ax2+2bx+c≥0在(-∞,+∞)内恒成立”,因此a>0,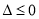 ,解得a∈[1,9].
,解得a∈[1,9].
试题解析:由f(x)=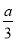 x3+bx2+cx+d得f′(x)=ax2+2bx+c
x3+bx2+cx+d得f′(x)=ax2+2bx+c
∵f′(x)-9x=ax2+2bx+c-9x=0的两根为1,4.
∴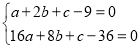 (*)
(*)
(1)当a=3时,由(*)式得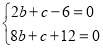 ,解得b=-3,c=12.
,解得b=-3,c=12.
又∵曲线y=f(x)过原点,∴d=0.
故f(x)=x3-3x2+12x.
(2)由于a>0,所以“f(x)=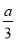 x3+bx2+cx+d在(-∞,+∞)内无极值点”等价于“f′(x)=ax2+2bx+c≥0在(-∞,+∞)内恒成立”,
x3+bx2+cx+d在(-∞,+∞)内无极值点”等价于“f′(x)=ax2+2bx+c≥0在(-∞,+∞)内恒成立”,
由(*)式得2b=9-5a,c=4a.
又∵Δ=(2b)2-4ac=9(a-1)(a-9)
解 ,得a∈[1,9],
,得a∈[1,9],
即a的取值范围为[1,9].
考点:1.函数与导函数的综合应用;2.不等式恒成立问题


科目:高中数学 来源:2015届内蒙古高二下学期期中考试理科数学试卷(解析版) 题型:选择题
用反证法证明命题“三角形的内角至多有一个钝角”时,假设正确的是( )
A.假设至少有一个钝角 B.假设至少有两个钝角
C.假设没有一个钝角 D.假设没有一个钝角或至少有两个钝角
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古包头市高二下学期期中Ⅰ理科数学试卷(解析版) 题型:选择题
函数y=f(x)在定义域(- ,3)内的图像如图所示.记y=f(x)的导函数为y=f?(x),则不等式f?(x)≤0的解集为( )
,3)内的图像如图所示.记y=f(x)的导函数为y=f?(x),则不等式f?(x)≤0的解集为( )

A.[- ,1]∪[2,3) B.[-1,
,1]∪[2,3) B.[-1, ]∪[
]∪[ ,
, ]
]
C.[- ,
, ]∪[1,2)D.(-
]∪[1,2)D.(- ,-
,-  ]∪[
]∪[ ,
, ]∪[
]∪[ ,3)
,3)
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古包头市高二下学期期中Ⅰ文科数学试卷(解析版) 题型:选择题
 是f(x)的导函数,
是f(x)的导函数, 的图象如下图所示,则f(x)的图象只可能是( )
的图象如下图所示,则f(x)的图象只可能是( )

(A) (B) (C) (D)
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知直线l经过点P(1,1),倾斜角为 ,且tan
,且tan =
=
(1)写出直线l的一个参数方程;
(2)设l与圆x2+y2=4相交于两点A,B,求点P到A,B两点的距离之积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com