解:(I)∵|PA|-|PB|=4<|AB|,∴动点P的轨迹是以A、B为焦点的双曲线的右支除去其与x轴的交点.
设双曲线方程为

.
由已知,得
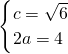
解得
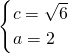
∴
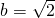
.
∴动点P的轨迹方程为

.
(5)由题意,直线MP(6)的斜率存在且不为0,设直线l的方程x=2.
设MP的方程为y=k(x+2).
∵点Q是l与直线MP的交点,∴Q(2,4k).设P(x
0,y
0)
由
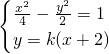
整理得(1-2k
2)x
2-8k
2x-(8k
2+4)=0.
则此方程必有两个不等实根x
1=-2,x
2=x
0>2∴1-2k
2≠0.,且

.
∴
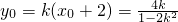
.∴

.
设T(t,0),要使得PN⊥QT,只需

由N(2,0),
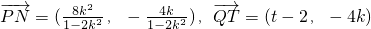
,
∴
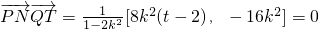
∵k≠0,∴t=4.此时

∴所求T的坐标为(4,0).
(III)由(II)知R(2,-4k),∴

=

,
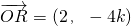
.
∴
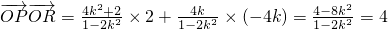
.
∴

.
说明其他正确解法按相应步骤给分.
(I)由题意可得,动点P的轨迹是以A、B为焦点的双曲线的右支除去其与x轴的交点.下面结合待定系数法求出双曲线方程即可;
(II)由题意,直线MP(6)的斜率存在且不为0,设直线l的方程x=2.设MP的方程为y=k(x+2),将直线的方程代入双曲线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用垂直条件即可求得所求T的坐标;
(III)由(II)知R(2,-4k),利用k表示出向量

,最后结合向量的数量积求出结果即得.
点评:直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.

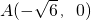 、
、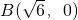 ,动点P满足|PA|=|PB|+4.
,动点P满足|PA|=|PB|+4.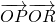 的值.
的值. .
.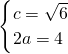 解得
解得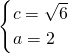
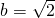 .
. .
.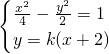 整理得(1-2k2)x2-8k2x-(8k2+4)=0.
整理得(1-2k2)x2-8k2x-(8k2+4)=0. .
.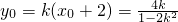 .∴
.∴ .
.
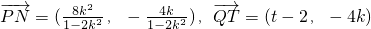 ,
,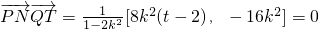

 =
= ,
,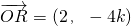 .
.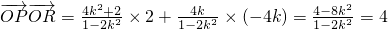 .
. .
. ,最后结合向量的数量积求出结果即得.
,最后结合向量的数量积求出结果即得.

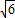 ,0)、B(
,0)、B(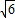 ,0),动点P满足|PA|=|PB|+4.
,0),动点P满足|PA|=|PB|+4.