
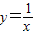 的图象为双曲线,在双曲线的两支上分别取点P,Q,则线段PQ的最小值为 ;
的图象为双曲线,在双曲线的两支上分别取点P,Q,则线段PQ的最小值为 ;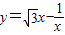 的图象为双曲线,在此双曲线的两支上分别取点P,Q,则线段PQ的最小值为 .
的图象为双曲线,在此双曲线的两支上分别取点P,Q,则线段PQ的最小值为 . 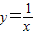 的实轴所在直线为y=x,再求y=x与双曲线的交点坐标,即可得到线段PQ的最小值.
的实轴所在直线为y=x,再求y=x与双曲线的交点坐标,即可得到线段PQ的最小值.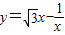 的实轴所在直线为y=(
的实轴所在直线为y=(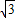 -2)x,再联解直线与双曲线方程,得到交点坐标后再用两点间的距离公式,可算出线段PQ的最小值.
-2)x,再联解直线与双曲线方程,得到交点坐标后再用两点间的距离公式,可算出线段PQ的最小值.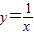 的图象为双曲线,两条渐近线分别为x轴和y轴
的图象为双曲线,两条渐近线分别为x轴和y轴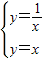 ,得交点为(1,1)和(-1,-1)
,得交点为(1,1)和(-1,-1)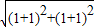 =2
=2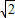
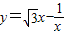 的导数为y′=
的导数为y′=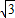 +
+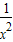 >
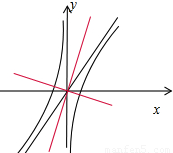
>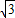 ,
,
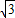 x,
x, -2)x,
-2)x,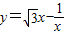 的交点为:
的交点为: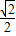 ,-
,- ),(-
),(-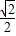 ,
,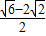 ),
),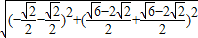 =2
=2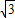 -2.
-2.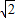 ,2
,2 -2
-2

科目:高中数学 来源:2012-2013学年浙江省重点中学高一(上)期中数学试卷(解析版) 题型:解答题
 的图象关于点(0,1)对称,求实数m的值;
的图象关于点(0,1)对称,求实数m的值;查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省重点中学高一(上)期中数学试卷(解析版) 题型:解答题
 的图象关于点(0,1)对称,求实数m的值;
的图象关于点(0,1)对称,求实数m的值;查看答案和解析>>
科目:高中数学 来源:2014届湖南长沙高二上第一学月理科数学试卷(解析版) 题型:填空题
(1)已知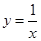 的图象为双曲线,在双曲线的两支上分别取点
的图象为双曲线,在双曲线的两支上分别取点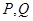 ,则线段
,则线段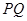 的最小值为 ;
的最小值为 ;
(2)已知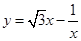 的图象为双曲线,在此双曲线的两支上分别取点
的图象为双曲线,在此双曲线的两支上分别取点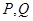 ,则线段
,则线段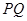 的最小值为 。
的最小值为 。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省长沙市南雅中学高二(上)第一次月考数学试卷(文科)(解析版) 题型:填空题
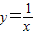 的图象为双曲线,在双曲线的两支上分别取点P,Q,则线段PQ的最小值为 ;
的图象为双曲线,在双曲线的两支上分别取点P,Q,则线段PQ的最小值为 ;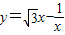 的图象为双曲线,在此双曲线的两支上分别取点P,Q,则线段PQ的最小值为 .
的图象为双曲线,在此双曲线的两支上分别取点P,Q,则线段PQ的最小值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com