
 (2015年1月•丰台期末•16)如图.某机器人的运动轨道是边长为1米的正三角形ABC.开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变-次运动方向(假设按此方式无限运动下去).运动过程中随时记录逆时针运动的总路程s1和顺时针运动的总路程s2.x为该机器人的“运动状态参数”,规定:逆时针运动时x=s1,顺时针运动时x=-s2.机器人到A点的距离d与x满足函数关系d=f(x).现有如下结论:
(2015年1月•丰台期末•16)如图.某机器人的运动轨道是边长为1米的正三角形ABC.开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变-次运动方向(假设按此方式无限运动下去).运动过程中随时记录逆时针运动的总路程s1和顺时针运动的总路程s2.x为该机器人的“运动状态参数”,规定:逆时针运动时x=s1,顺时针运动时x=-s2.机器人到A点的距离d与x满足函数关系d=f(x).现有如下结论:分析 根据问题的情景,对自变量x分类讨论,当x∈[0,3]时,分成三段,当x∈[-3,0)也分成三段,再根据所确定的函数式,画出函数f(x)的图象,最后根据图象确定各说法的正误.
解答 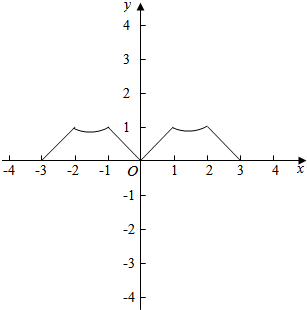 解:∵x∈[0,3]时,点P作逆时针运动,分段如下:
解:∵x∈[0,3]时,点P作逆时针运动,分段如下:
(1)当x∈[0,1],点P在AB上,f(x)=x;
(2)当x∈(1,2],点P在BC上,在△ABP中运用余弦定理,f(x)=$\sqrt{x^2-3x+3}$;
(3)当x∈(2,3]时,点P在CA上,f(x)=3-x,
又∵x∈[-3,0)时,点P作顺时针运动,函数时求解方法同上,
(1)当x∈[-1,0),点P在AC上,f(x)=-x;
(2)当x∈[-2,-1),点P在BC上,在△ACP中运用余弦定理,f(x)=$\sqrt{x^2+3x+3}$;
(3)当x∈[-3,-2)时,点P在BA上,f(x)=3-x,
根据以上分析,画出函数f(x)的图象,如右图,显然:
①正确;
②正确;
③错误,该函数为偶函数;
④正确.
故填:①②④.
点评 本题主要考查了函数解析式的求法,分段函数的性质,涉及奇偶性,周期性,值域及单调性和单调区间,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤1或a≥$\frac{9}{2}$ | B. | a≤$\frac{4}{3}$或a≥$\frac{7}{2}$ | C. | a≤1或a≥$\frac{7}{2}$ | D. | a≤$\frac{4}{3}$或a≥$\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com