
| A.50 | B.54 | C.58 | D.60 |
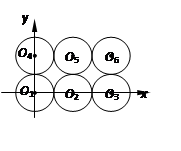
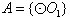 ,则集合
,则集合 是集合
是集合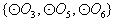 的非空子集,有
的非空子集,有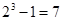 种可能。
种可能。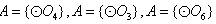 的情况类似,则总共有4×7=28个“有序集合对”;
的情况类似,则总共有4×7=28个“有序集合对”;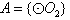 ,则集合
,则集合 是集合
是集合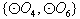 的非空子集,有
的非空子集,有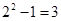 种可能。
种可能。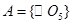 的情况类似,则总共有2×3=6个“有序集合对”;
的情况类似,则总共有2×3=6个“有序集合对”;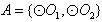 ,则集合
,则集合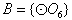 只有1种可能。
只有1种可能。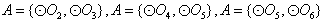 的情况类似,则总共有4×1=4个“有序集合对”;
的情况类似,则总共有4×1=4个“有序集合对”;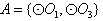 ,则集合
,则集合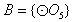 只有1种可能。
只有1种可能。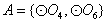 的情况类似,则总共有2×1=2个“有序集合对”;
的情况类似,则总共有2×1=2个“有序集合对”;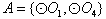 ,则集合
,则集合 是集合
是集合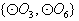 的非空子集,有
的非空子集,有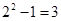 种可能。
种可能。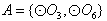 的情况类似,而
的情况类似,而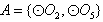 与其他圆均有公共点此时不存在集合
与其他圆均有公共点此时不存在集合 ,则总共有2×3=6个“有序集合对”;
,则总共有2×3=6个“有序集合对”;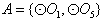 ,则集合
,则集合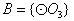 只有1种可能。
只有1种可能。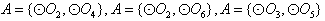 的情况类似,则总共有4×1=4个“有序集合对”;
的情况类似,则总共有4×1=4个“有序集合对”;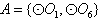 ,此时与其他圆均有公共点此时不存在集合
,此时与其他圆均有公共点此时不存在集合 。
。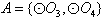 的情况类似,则总共有0个“有序集合对”;
的情况类似,则总共有0个“有序集合对”;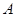 中有3个元素时,则只有当,
中有3个元素时,则只有当,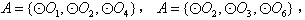
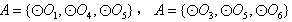 情况下,集合
情况下,集合 对应有1种可能,其他情况下均与其他圆均有公共点此时不存在集合
对应有1种可能,其他情况下均与其他圆均有公共点此时不存在集合 。则总共有4×1=4个“有序集合对”;
。则总共有4×1=4个“有序集合对”; 中有4个以上元素时,均与其他圆均有公共点此时不存在集合
中有4个以上元素时,均与其他圆均有公共点此时不存在集合 。则不存在“有序集合对”。
。则不存在“有序集合对”。

科目:高中数学 来源:不详 题型:单选题
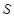 是实数集
是实数集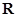 的非空子集,如果
的非空子集,如果 有
有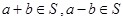 ,则称
,则称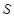 是
是A.存在有限集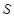 , ,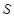 是一个“和谐集” 是一个“和谐集” |
B.对任意无理数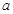 ,集合 ,集合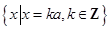 都是“和谐集” 都是“和谐集” |
C.若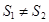 ,且 ,且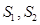 均是“和谐集”,则 均是“和谐集”,则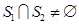 |
D.对任意两个“和谐集”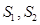 ,若 ,若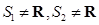 ,则 ,则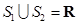 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com