Question

设直线的方程为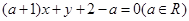
（1）若直线在两坐标轴上的截距相等，则直线的方程是      　 ；
（2）若直线不经过第二象限，则实数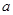的取值范围是     ．

Answer 1

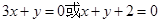（1） （2） 

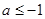
解析试题分析：（Ⅰ）直线方程为l：（a+1）x+y+2-a=0（a∈R），令x=0可得 y=a-2；令y=0可得x=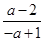，若直线l在两坐标轴上的截距相等，则a-2=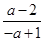
，解得 a=2或 a=-2，故直线l方程为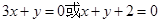
（Ⅱ）∵直线方程为 y=-（a+1）x+a-2，若l不经过第二象限，则a="2" 或-(a+1)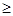0，a-2≤0
解得a≤-1，故实数a的取值范围为a≤-1。
考点：本题主要是考查直线方程的一般式，直线在坐标轴上的截距的定义，直线在坐标系中的位置与它的斜率、截距的关系，属于基础题．
点评：解决该试题的关键是根据直线方程求出它在两坐标轴上的截距，根据它在两坐标轴上的截距相等，求出a的值，即得直线l方程，第二问把直线方程化为斜截式为 y=-（a+1）x-a-2，若l不经过第二象限，则可以考虑两种情况结合截距来得到。