数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
【答案】
分析:(1)先由a
n+1=2S
n+1求出a
n+1=3a
n.再利用数列{a
n}为等比数列,可得a
2=3a
1.就可以求出t值.
(2)先利用T
3=15求出b
2=5,,再利用公差把b
1和b
3表示出来.代入a
1+b
1,a
2+b
2,a
3+b
3成等比数列,求出公差即可求T
n.
解答:解:(1)由a
n+1=2S
n+1 ①可得a
n=2s
n-1+1 (n≥2)②
两式作差得 a
n+1-a
n=2a
n⇒a
n+1=3a
n.
因为数列{a
n}为等比数列⇒a
2=2s
1+1=2a
1+1=3a
1⇒a
1=t=1.
所以数列{a
n}是首项为1,公比为3的等比数列
∴a
n=3
n-1.
(2)设等差数列{b
n}的公差为d,
由T
3=15⇒b
1+b
2+b
3=15⇒b
2=5,
所以可设b
1=5-d,b
3=5+d.
又a
1=1,a
2=3,a
3=9.
由题得(5-d+1)(5+d+9)=(5+3)
2.⇒d=-10,d=2.
因为等差数列{b
n}的前n项和T
n有最大值,且b
2=5,所以d=-10.
解得b
1=15,
所以T
n=15n+
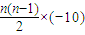
=20n-5n
2.
点评:本题综合考查等差数列和等比数列的知识.对于等差数列,要想前n项和有最大值,必须是递减数列,即公差为负数.

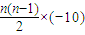 =20n-5n2.
=20n-5n2.

 小学教材完全解读系列答案
小学教材完全解读系列答案