
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且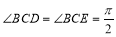 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
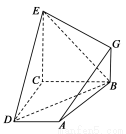
(1)求证: EC⊥CD ;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
(1)证明过程详见解析;(2)证明过程详见解析;(3)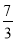
【解析】
试题分析:(1)要证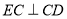 ,只要证
,只要证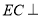 平面
平面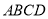 ;而由题设平面
;而由题设平面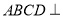 平面
平面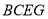 且
且 ,所以
,所以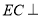 平面
平面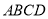 ,结论得证;
,结论得证;
(2)过G作GN⊥CE交BE于M,连 DM,由题设可证四边形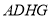 为平行四边形,所以有
为平行四边形,所以有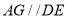
从而由直线与平面平行的判定定理,可证AG∥平面BDE;
(3)欲求几何体EG-ABCD的体积,可先将该几何体分成一个四棱锥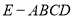 和三棱锥
和三棱锥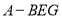 .
.
试题解析:
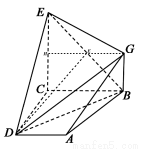
(1)证明:由平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC, 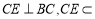 平面BCEG,
平面BCEG,
 EC⊥平面ABCD,3分
EC⊥平面ABCD,3分
又CD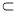 平面BCDA, 故 EC⊥CD4分
平面BCDA, 故 EC⊥CD4分
(2)证明:在平面BCDG中,过G作GN⊥CE交BE于M,连DM,则由已知知;MG=MN,MN∥BC∥DA,且
 MG∥AD,MG=AD, 故四边形ADMG为平行四边形,
MG∥AD,MG=AD, 故四边形ADMG为平行四边形,
 AG∥DM6分
AG∥DM6分
∵DM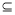 平面BDE,AG
平面BDE,AG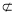 平面BDE,
平面BDE,  AG∥平面BDE8分
AG∥平面BDE8分
(3)【解析】 10分
10分
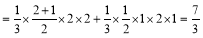 12分
12分
考点:1、直线与平面垂直、平行的判定与性质;2、空间几何体的体积.


科目:高中数学 来源:2013-2014学年山东省高三12月月考文科数学试卷(解析版) 题型:选择题
“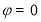 ”是“函数
”是“函数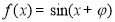 为奇函数”的( )
为奇函数”的( )
A.充分非必要条件 B. 必要非充分条件
C.充要条件 D. 非充分非必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试理科数学试卷(解析版) 题型:选择题
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8 ;
④对分类变量X与Y的随机变量k2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.
其中真命题的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试文科数学试卷(解析版) 题型:填空题
设关于x,y的不等式组 表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是
表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试文科数学试卷(解析版) 题型:选择题
某程序框图如图2所示,现将输出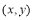 值依次记为:
值依次记为: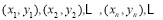 若程序运行中输出的一个数组是
若程序运行中输出的一个数组是 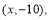 则数组中的
则数组中的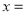 ( )
( )
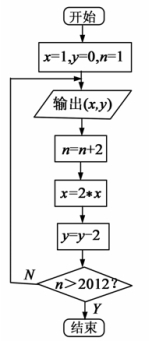
A.32 B.24 C.18 D.16
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:填空题
若数列 满足:存在正整数
满足:存在正整数 ,对于任意正整数
,对于任意正整数 都有
都有 成立,则称数列
成立,则称数列 为周期数列,周期为
为周期数列,周期为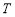 . 已知数列
. 已知数列 满足
满足 ,
,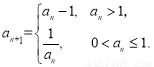 现给出以下命题:
现给出以下命题:
①若 ,则
,则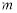 可以取3个不同的值
可以取3个不同的值
②若 ,则数列
,则数列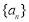 是周期为
是周期为 的数列
的数列
③ 且
且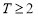 ,存在
,存在 ,
, 是周期为
是周期为 的数列
的数列
④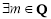 且
且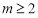 ,数列
,数列 是周期数列.其中所有真命题的序号是 .
是周期数列.其中所有真命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com