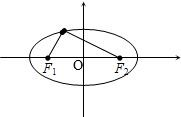
分析:先根据椭圆的标准方程,求得半焦距c,进而根据椭圆的定义求得|MF1|+|MF2|的值,进而利用余弦定理求得|MF1|和|MF2|的关系式,联立方程求得|MF1|和|MF2|,最后根据三角形面积公式求得三角形的面积.
解答:解:由
+
=1,得a=8,b=6,c=
=2
.
根据椭圆定义,有|MF
1|+|MF
2|=2a=16.
在△F
1MF
2中,由余弦定理,得到
|F
1F
2|
2=|MF
1|
2+|MF
2|
2-2|MF
1|•|MF
2|•cos∠F
1MF
2.
即
(4)2=|MF
1|
2+|MF
2|
2-2|MF
1|•|MF
2|•cos60°,
112═|MF
1|
2+|MF
2|
2-|MF
1|•|MF
2|=(|MF
1|+|MF
2|)
2-3|MF
1|•|MF
2|=16
2-3|MF
1|•|MF
2|,
解得|MF
1|=|MF
2|=48.
△F
1MF
2的面积为:S=
|MF
1|•|MF
2|sin∠F
1MF
2=
×48×sin60°=12
.
点评:本题主要考查了椭圆的应用.特别是利用椭圆的定义解决椭圆的实际问题.