
分析 根据三角形的周长和定点,得到点A到两个定点的距离之和等于定值,得到点C的轨迹是椭圆,椭圆的焦点在x轴上,写出椭圆的方程,去掉不合题意的点.
解答 解:∵△ABC的两顶点A(-1,0),B(1,0),△ABC周长为6,
∴AB=2,BC+AC=4,
∵4>2,∴点C到两个定点的距离之和等于定值,点C满足椭圆的定义,
∴点C的轨迹是以A,B为焦点的椭圆(除去椭圆与x轴的交点),
∴2a=4,2c=2,∴a=2,c=1,b=$\sqrt{3}$,
∴椭圆的标准方程是$\frac{x^2}{4}+\frac{y^2}{3}=1({y≠0})$,
故答案为以A,B为焦点的椭圆(除去椭圆与x轴的交点),方程为$\frac{x^2}{4}+\frac{y^2}{3}=1({y≠0})$.
点评 本题考查轨迹方程的求法,注意椭圆的定义的应用是关键.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 老年人应作为重点调查对象,故抽取的老年人应超过40名 | |
| B. | 每个人被抽到的概率相同为$\frac{1}{10}$ | |
| C. | 应使用分层抽样抽取样本调查 | |
| D. | 抽出的样本能在一定程度上反映总体的健康状况 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 12 | D. | -12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 4 | C. | 3 | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
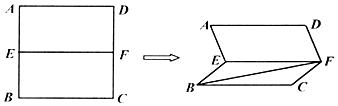 如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.
如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com