练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

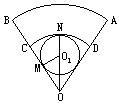
    一扇形铁皮AOB，半径OA＝72cm，圆心角∠AOB＝，现剪下一个扇环ABCD做圆台形容器的侧面，并从剩余的扇形COD内剪下一个最大的圆刚好做容器的下底(圆台下底面大于上底面)(如图)，则OC应取多少？

    答案：
    解析：

    解:设OC＝xcm，圆台下底面半径为r，即＝r．∠CON＝∠AOB＝，∴＝2r，ON＝＝3r，∴r＝x．由2πr与长相等得2πr＝·2π·72，∴r＝12，故x＝3r＝36(cm)．即OC应取36cm．

    说明:本题可以进而计算圆台形容器的最大容积及其侧面积等．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，现有一块半径为2m，圆心角为90°的扇形铁皮AOB，欲从其中裁剪出一块内接五边形
    ONPQR，使点P在AB弧上，点M，N分别在半径OA和OB上，四边形PMON是矩形，点Q在弧AP上，R点在线段AM上，四边形PQRM是直角梯形．现有如下裁剪方案：先使矩形PMON的面积达到最大，在此前提下，再使直角梯形PQRM的面积也达到最大．
    （Ⅰ）设∠BOP=θ，当矩形PMON的面积最大时，求θ的值；
    （Ⅱ）求按这种裁剪方法的原材料利用率．

    查看答案和解析>>

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：022

    一扇形铁皮AOB，半径OA＝72cm，圆心角∠AOB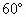＝，现剪下一个扇环ABCD做圆台形容器的侧面，并从剩下的扇形OCD内剪下一个最大的圆刚好做容器的下底(圆台的下底面大于上底面)(如图)，则OC的长为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

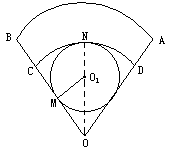
    一扇形铁皮AOB,半径OA=72 cm,圆心角∠AOB=60°.现剪下一个扇环ABCD作圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好作容器的下底(圆台的下底面大于上底面),则OC的长为______________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    一扇形铁皮AOB,半径OA="72" cm,圆心角∠AOB=60°.现剪下一个扇环ABCD作圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好作容器的下底(圆台的下底面大于上底面),则OC的长为________.

    查看答案和解析>>

    同步练习册答案