
【题目】如图(1)在等腰直角三角形![]() 中,
中,![]() ,将
,将![]() 沿中位线
沿中位线![]() 翻折得到如图(2)所示的空间图形,使二面角
翻折得到如图(2)所示的空间图形,使二面角![]() 的大小为
的大小为![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)证明![]() ∥
∥![]() ,
,![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,由面面垂直的判定定理即可证出平面
,由面面垂直的判定定理即可证出平面![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,所以
,所以![]() ,由(1)可知平面
,由(1)可知平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以以
,所以以![]() 为原点建立如图所示空间直角坐标系,则
为原点建立如图所示空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,利用空间向量法求解即可.
,利用空间向量法求解即可.
(1)由题意可知![]() 为
为![]() 的中位线,所以
的中位线,所以![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因为图(2)所示的空间图形是由![]() 沿中位线
沿中位线![]() 翻折得到的,
翻折得到的,
所以![]() ,
,![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)由(1)可知二面角![]() 的平面角即为
的平面角即为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 为等边三角形,
为等边三角形,
如图取![]() 的中点
的中点![]() ,所以
,所以![]() ,由(1)可知平面
,由(1)可知平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以以
,所以以![]() 为原点建立如图所示空间直角坐标系,
为原点建立如图所示空间直角坐标系,
设图1等腰直角![]() 中
中![]() ,则图2中
,则图2中![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以有 ,即
,即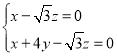 ,取
,取![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以 ,
,
所以直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】用6个字母![]() 编拟某种信号程序(大小写有区别),把这6个字母全部排列如图所示的表格中,每个字母必须使用且只使用一次,不同的排列方式表示不同的信号,如果恰有一对字母(同一个字母的大小写)排到同一列的上下格位置,那么称此信号为“微错号”,则不同的“微错号”的总数为( )
编拟某种信号程序(大小写有区别),把这6个字母全部排列如图所示的表格中,每个字母必须使用且只使用一次,不同的排列方式表示不同的信号,如果恰有一对字母(同一个字母的大小写)排到同一列的上下格位置,那么称此信号为“微错号”,则不同的“微错号”的总数为( )
A.144B.288C.432D.576
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两个不重合的平面,下列选项中,一定能得出平面
是两个不重合的平面,下列选项中,一定能得出平面![]() 与平面
与平面![]() 平行的是( )
平行的是( )
A.平面![]() 内有一条直线与平面
内有一条直线与平面![]() 平行
平行
B.平面![]() 内有两条直线与平面
内有两条直线与平面![]() 平行
平行
C.平面![]() 内有一条直线与平面
内有一条直线与平面![]() 内的一条直线平行
内的一条直线平行
D.平面![]() 与平面
与平面![]() 不相交
不相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司在![]() 年年初准备将
年年初准备将![]() 万元投资到“低碳”项目上,现有两个项目供选择:
万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利![]() ,也可能亏损
,也可能亏损![]() ,且这两种情况发生的概率分别为
,且这两种情况发生的概率分别为![]() 和
和![]() ;
;
项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利![]() ,可能损失
,可能损失![]() ,也可能不赔不赚,且这三种情况发生的概率分别为
,也可能不赔不赚,且这三种情况发生的概率分别为![]() 、
、![]() 和
和![]() .
.
针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com