甲乙两个盒子里各放有标号为1,2,3,4的四个大小形状完全相同的小球,从甲盒中任取一小球,记下号码x后放入乙盒,再从乙盒中任取一小球,记下号码y,设随机变量X=|x-y|.
(1)求y=2的概率;
(2)求随机变量X的分布列及数学期望.
分析:(1)由题意知y=2 包括两种情况,一是x=2,y=2,一是x≠2,y=2,根据变量的结果对应的事件做出两种情况的概率,这两种情况是互斥的,且每一种情况中包含的事件是相互独立事件,根据公式得到结果.
(2)由题意知随机变量的取值是0、1、2、3,根据不同变量对应的事件得到概率,写出分布列和期望,不同是一个必得分的题目.
解答:解:(1)由题意知y=2 包括两种情况,一是x=2,y=2,一是x≠2,y=2,
∴P(y=2)=P(x=2,y=2)+P(x≠2,y=2)=
×+×=(2)随机变量X可取的值为0,1,2,3
当X=0时,(x,y)=(1,1),(2,2),(3,3),(4,4)
∴
P(X=0)=×+×+×+×=当X=1时,(x,y)=(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)
∴
P(X=1)=×-×+×-×-×+×=同理可得
P(X=2)=;P(X=3)=∴随机变量X的分布列为
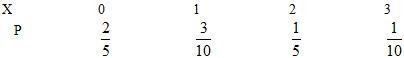
∴
EX=0×+1×+2×+3×=1 点评:本题考查离散型随机变量的分布列和期望,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道大题,文科考概率一般考查古典概型和几何概型.

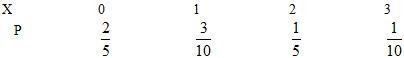


 发散思维新课堂系列答案
发散思维新课堂系列答案 后放入乙盒,再从乙盒中任取一小球,记下号码
后放入乙盒,再从乙盒中任取一小球,记下号码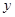 ,设随机变量
,设随机变量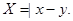
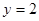 的概率;
的概率;