
甲乙两个盒子里各放有标号为1,2,3,4的四个大小形状完全相同的小球,从甲盒中任取一小球,记下号码x后放入乙盒,再从乙盒中任取一小球,记下号码y,设随机变量X=|x﹣y|.
(1)求y=2的概率;
(2)求随机变量X的分布列及数学期望.
考点:
等可能事件的概率;离散型随机变量及其分布列;离散型随机变量的期望与方差.
专题:
计算题.
分析:
(1)由题意知y=2 包括两种情况,一是x=2,y=2,一是x≠2,y=2,根据变量的结果对应的事件做出两种情况的概率,这两种情况是互斥的,且每一种情况中包含的事件是相互独立事件,根据公式得到结果.
(2)由题意知随机变量的取值是0、1、2、3,根据不同变量对应的事件得到概率,写出分布列和期望,不同是一个必得分的题目.
解答:
解:(1)由题意知y=2 包括两种情况,一是x=2,y=2,一是x≠2,y=2,
∴P(y=2)=P(x=2,y=2)+P(x≠2,y=2)=![]()
(2)随机变量X可取的值为0,1,2,3
当X=0时,(x,y)=(1,1),(2,2),(3,3),(4,4)
∴![]()
当X=1时,(x,y)=(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)
∴![]()
同理可得![]()
∴随机变量X的分布列为
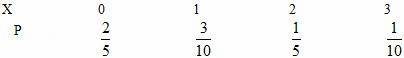
∴![]()
点评:
本题考查离散型随机变量的分布列和期望,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道大题,文科考概率一般考查古典概型和几何概型.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省皖南八校高三第一次联考理科数学卷 题型:解答题
(本小题满分12分)
甲乙两个盒子里各放有标号为1,2,3,4的四个大小形状完全相同的小球,从甲盒中任取一小球,记下号码 后放入乙盒,再从乙盒中任取一小球,记下号码
后放入乙盒,再从乙盒中任取一小球,记下号码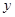 ,设随机变量
,设随机变量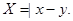
(1)求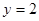 的概率;
的概率;
(2)求随机变量X的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市盱眙县马坝中学高三(下)期初数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市高三(下)毕业班冲刺训练数学试卷2(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com