
(09年海淀区期末文)(14分)
直三棱柱A1B1C1―ABC中,![]()
(I)求证:BC1//平面A1CD;
(II)求二面角A―A1C―D的大小。

解析:(I)证明:连结AC1,设![]() 连结DE,…………1分
连结DE,…………1分
![]() A1B1C1―ABC是直三棱柱,且
A1B1C1―ABC是直三棱柱,且![]()
![]() AA1CC1是正方形,E是AC1的中点,
AA1CC1是正方形,E是AC1的中点,
又D为AB中点,
![]() ED//BC1…………3分
ED//BC1…………3分
又![]()
![]() BC1//平面A1CD…………5分
BC1//平面A1CD…………5分
(II)法一:设H是AC中点,F是EC中点,连接DH,HF,FD…………6分
|
![]() D为AB中点,
D为AB中点,
![]() DH//BC,同理可证HF//AE,
DH//BC,同理可证HF//AE,
又![]()
又侧棱![]()
![]()
![]() …………8分
…………8分
由(I)得AA1C1C是正方形,则![]()
![]()
![]() 在平面AA1C1C上的射影,
在平面AA1C1C上的射影,
![]()
![]() 是二面角A―A1C―D的平面角…………10分
是二面角A―A1C―D的平面角…………10分
又![]() ……12分
……12分
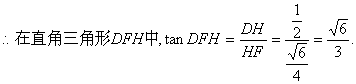 …………13分
…………13分
![]() …………14分
…………14分
法二:在直三棱柱A1B1C1―ABC中,
![]() 分别以CA,CB,CC1所在的直线为
分别以CA,CB,CC1所在的直线为![]() 建立空间直角坐标系,
建立空间直角坐标系,
![]()
则![]() ……7分
……7分
|
设平面A1DC的法向量为![]() 则
则
 …………8分
…………8分
![]()
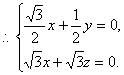
则 …………9分
…………9分
取![]() ……10分
……10分
![]() 为平面CAA1C1的一个法向量…………11分
为平面CAA1C1的一个法向量…………11分
![]() …………12分
…………12分
由图可知,二面角A―A1C―D的大小为![]() …………14分
…………14分


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
(09年海淀区期末文)(14分)
已知椭圆![]() A1、A2、B是椭圆的顶点(如图),直线
A1、A2、B是椭圆的顶点(如图),直线![]() 与椭圆交于异于椭圆顶点的P、Q两点,且
与椭圆交于异于椭圆顶点的P、Q两点,且![]() //A2B。若此椭圆的离心率为
//A2B。若此椭圆的离心率为![]()
(I)求此椭圆的方程;
(II)设直线A1P和直线BQ的倾斜角分别为![]() 是否为定值?若是,求出此定值;若不是,请说明理由。
是否为定值?若是,求出此定值;若不是,请说明理由。

查看答案和解析>>
科目:高中数学 来源: 题型:
(09年海淀区期末文)(14分)
某种家用电器每台的销售利润与该电器的无故障使用时间有关,每台这种家用电器若无故障使用时间不超过一年,则销售利润为0元,若无故障使用时间超过一年不超过三年,则销售利润为100元;若无故障使用时间超过三年,则销售利润为200元。
已知每台该种电器的无故障使用时间不超过一年的概率为![]() 无故障使用时间超过一年不超过三年的概率为
无故障使用时间超过一年不超过三年的概率为![]()
(I)求销售两台这种家用电器的销售利润总和为400元的概率;
(II)求销售三台这种家用电器的销售利润总和为300元的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com