
分析 (1)利用直线垂直与斜率之间的关系可得a,进而得到直线的交点.
(2)利用平行与斜率之间的关系可得a,再利用平行线之间的距离公式即可得出.
解答 解:由2x+y+4=0,得y=-2x+4,所以直线l1的斜率为k1=-2;
同理求得直线l2的斜率为${k_2}=-\frac{a}{4}$…(1分)
(1)当l1⊥l2时,k1k2=-1,∴$(-2)×(-\frac{a}{4})=-1$,解得a=-2.
此时,l2:-2x+4y+1=0.
由$\left\{\begin{array}{l}2x+y+4=0,\;\;\\-2x+4y+1=0\end{array}\right.$解得$\left\{\begin{array}{l}x=-\frac{3}{2},\;\;\\ y=-1.\end{array}\right.$
∴l1与l2的交点坐标为$(-\frac{3}{2},-1)$…(5分)
(2)当l1∥l2时,k1=k2,∴$-2=-\frac{a}{4}$,解得a=8.
此时,l2:8x+4y+1=0,l1可化为8x+4y+16=0.
由两平行线间距离公式得l1与l2间的距离为$d=\frac{|16-1|}{{\sqrt{{8^2}+{4^2}}}}=\frac{15}{{4\sqrt{5}}}=\frac{{3\sqrt{5}}}{4}$…(10分)
点评 本题考查了直线平行垂直与斜率之间的关系、平行线之间的距离公式、直线交点,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 32π | C. | 36π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,-2) | B. | (2,2) | C. | (-2,-2) | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |f(x)|g(x)是奇函数 | B. | f(x)g(x)是偶函数 | C. | f(x)|g(x)|是奇函数 | D. | |f(x)g(x)|是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
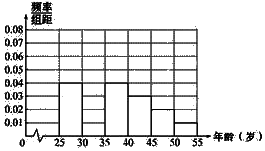 我校高二同学利用暑假进行了社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
我校高二同学利用暑假进行了社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:| 组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 18 | C. | 12 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com