
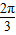 ,弧长为2π,则其面积为3π;
,弧长为2π,则其面积为3π;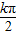 ,k∈Z};
,k∈Z};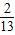 ;
;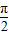 )在(0,π)上是减函数;
)在(0,π)上是减函数;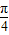 )在(
)在(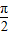 ,π)上单调递减,则ω的取值范围是[
,π)上单调递减,则ω的取值范围是[ ,
, ].
].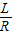 弧度可得半径R,由扇形的面积公式可得:S=
弧度可得半径R,由扇形的面积公式可得:S= LR;
LR;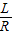 =(弧度),从而R=
=(弧度),从而R=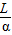 =
=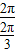 =3.
=3. LR=
LR= ×2π×3=3π,故①正确.
×2π×3=3π,故①正确.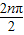 =nπ,表示的是终边在x轴上的角,故②不正确;
=nπ,表示的是终边在x轴上的角,故②不正确;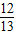 +2×
+2×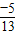 =
=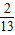 .故③正确;
.故③正确;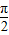 )=-cosx,又函数y=cosx在区间(0,π)上单调递减,
)=-cosx,又函数y=cosx在区间(0,π)上单调递减,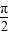 )=-cosx在区间(0,π)是单调递增,故④不正确.
)=-cosx在区间(0,π)是单调递增,故④不正确.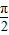 )≤π?ω≤2,(ωx+
)≤π?ω≤2,(ωx+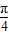 )∈[
)∈[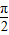 ω+
ω+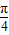 ,πω+
,πω+ ]?[
]?[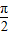 ,
, ]
]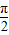 ω+
ω+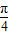 ≥
≥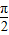 ,πω+
,πω+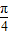 ≤
≤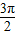 ?
? ≤ω≤
≤ω≤ .正确.
.正确.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 2π |
| 3 |
| kπ |
| 2 |
| 2 |
| 13 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 ,弧长为2π,则其面积为3π;
,弧长为2π,则其面积为3π; ,k∈Z};
,k∈Z};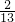 ;
; )在(0,π)上是减函数;
)在(0,π)上是减函数; )在(
)在( ,π)上单调递减,则ω的取值范围是[
,π)上单调递减,则ω的取值范围是[ ,
, ].
].查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 2π |
| 3 |
| kπ |
| 2 |
| 2 |
| 13 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com