练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知半径为的球面上有两点，且，球心为，若是球面上的动点，且二面角的大小为，则四面体的外接球表面积为______.

    【答案】

    【解析】

    设所在截面圆的圆心为，中点为，连接，易知，，从而可知即为二面角的平面角，，进而可求出，，，由到三点的距离相等，可知四面体外接球的球心在射线上，设四面体外接球半径为，在中，由勾股定理，可得，可求出，进而求出外接球的表面积.

    设所在截面圆的圆心为，中点为，连接，

    则，所以，同理，所以即为二面角的平面角，.

    因为，，所以是等腰直角三角形，所以.

    在中，由，得，由勾股定理，得.

    因为到三点的距离相等，所以四面体外接球的球心在射线上.

    设四面体外接球半径为，在中，，，，由勾股定理，可得，即，解得，所以.

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】江苏省从2021年开始，高考取消文理分科，实行“3＋1＋2”的模式，其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目，某校为了解高一年级学生对“1”的选课情况，随机抽取了100名学生进行问卷调查，如下表是根据调查结果得到的2×2列联表.

    性别

    选择物理

    选择历史

    总计

    男生

    50

    b

    m

    女生

    c

    20

    40

    总计

    100

    （1）求m，b，c的值；

    （2）请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关？说明你的理由.

    附：对于2×2列联表

    类1

    类2

    合计

    类A

    a

    b

    a＋b

    类B

    c

    d

    c＋d

    合计

    a＋c

    b＋d

    a＋b＋c＋d

    有，其中.

    P()

    0.100

    0.050

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数f(x)满足f(x＋2)＝f(x)，且当x∈[－1，1]时，f(x)＝x2.令g(x)＝f(x)－kx－k，若在区间[－1，3]内，函数g(x)＝0有4个不相等实根，则实数k的取值范围是(　　)

    A.(0，＋∞)B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】边长为2正方体中，点E在棱CD上.

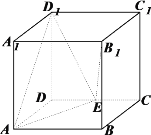
    （1）求证：；

    （2）若E是CD中点，求与平面所成的角的正弦值；

    （3）设M在棱上，且，是否存在点E，使平面⊥平面，若存在，指出点E的位置，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“爱国，是人世间最深层、最持久的情感，是一个人立德之源、立功之本。”在中华民族几千年绵延发展的历史长河中，爱国主义始终是激昂的主旋律。爱国汽车公司拟对“东方红”款高端汽车发动机进行科技改造，根据市场调研与模拟，得到科技改造投入（亿元）与科技改造直接收益（亿元）的数据统计如下：

    2

    3

    4

    6

    8

    10

    13

    21

    22

    23

    24

    25

    13

    22

    31

    42

    50

    56

    58

    68.5

    68

    67.5

    66

    66

    当时，建立了与的两个回归模型：模型①：；模型②：；当时，确定与满足的线性回归方程为：.

    （1）根据下列表格中的数据，比较当时模型①、②的相关指数，并选择拟合精度更高、更可靠的模型，预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.

    回归模型

    模型①

    模型②

    回归方程

    182.4

    79.2

    （附：刻画回归效果的相关指数，.）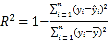

    （2）为鼓励科技创新，当科技改造的投入不少于20亿元时，国家给予公司补贴收益10亿元，以回归方程为预测依据，比较科技改造投入17亿元与20亿元时公司实际收益的大小；

    （附：用最小二乘法求线性回归方程的系数公式 ；）

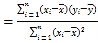    （3）科技改造后，“东方红”款汽车发动机的热效率大幅提高，服从正态分布，公司对科技改造团队的奖励方案如下：若发动机的热效率不超过，不予奖励；若发动机的热效率超过但不超过，每台发动机奖励2万元；若发动机的热效率超过，每台发动机奖励5万元.求每台发动机获得奖励的数学期望.

    （附：随机变量服从正态分布，则，.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一批产品共10件，其中3件是不合格品，用下列两种不同方式从中随机抽取2件产品检验：

    方法一：一次性随机抽取2件；

    方法二：先随机抽取1件，放回后再随机抽取1件.

    记方法一抽取的不合格产品数为.记方法二抽取的不合格产品数为.

    （1）求两种抽取方式下，的概率分布列；

    （2）比较两种抽取方式抽到的不合格品平均数的大小？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求的图象在处的切线方程；

    （2）当时，求证：在上有唯一零点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年春节期间，某超市准备举办一次有奖促销活动，若顾客一次消费达到400元则可参加一次抽奖活动，超市设计了两种抽奖方案.

    方案一：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得60元的返金券，若抽到白球则获得20元的返金券，且顾客有放回地抽取3次.

    方案二：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得80元的返金券，若抽到白球则未中奖，且顾客有放回地抽取3次.

    （1）现有两位顾客均获得抽奖机会，且都按方案一抽奖，试求这两位顾客均获得180元返金券的概率；

    （2）若某顾客获得抽奖机会.

    ①试分别计算他选择两种抽奖方案最终获得返金券的数学期望；

    ②为了吸引顾客消费，让顾客获得更多金额的返金券，该超市应选择哪一种抽奖方案进行促销活动？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数在区间上单调，求的取值范围；

    （2）若函数在上无零点，求的最小值.

    查看答案和解析>>

    同步练习册答案