
已知函数![]() 在x=±1处取得极值
在x=±1处取得极值
(1)求函数![]() 的解析式;
的解析式;
(2)求证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有![]() ≤4;
≤4;
(3)若过点A(1,m)(m ≠-2)可作曲线![]() 的三条切线,求实数m的范围。
的三条切线,求实数m的范围。
解:(1)![]() =3ax2+2bx-3,依题意,f′(1)=f′(-1)=0,
=3ax2+2bx-3,依题意,f′(1)=f′(-1)=0,
即![]() ………………… 2分
………………… 2分
解得a=1,b=0.∴f(x)=x3-3x. ……………………… 4分
(2)∵f(x)=x3-3x,∴f ′(x)=3x2-3=3(x+1)(x-1),
当-1<x<1时,f ′ (x)<0,故f(x)在区间[-1,1]上为减函数,
fmax(x)=f(-1)=2,fmin(x)=f(1)=-2 …………………… 6分
∵对于区间[-1,1]上任意两个自变量的值x1,x2,
都有|f(x1)-f(x2)|≤|fmax(x) -fmin(x)|
|f(x1)-f(x2)|≤|fmax(x)-fmin(x)|=2-(-2)=4 ……………… 8分
(3)f′(x)=3x2-3=3(x+1)(x-1),
∵曲线方程为y=x3-3x,∴点A(1,m)不在曲线上.
设切点为M(x0,y0),则点M的坐标满足![]()
因![]() ,故切线的斜率为
,故切线的斜率为![]() ,
,
整理得![]() .
.
∵过点A(1,m)可作曲线的三条切线,
∴关于x0方程![]() =0有三个实根. ……………… 10分
=0有三个实根. ……………… 10分
设g(x0)= ![]() ,则g′(x0)=6
,则g′(x0)=6![]() ,
,
由g′(x0)=0,得x0=0或x0=1.
∴g(x0)在(-∞,0),(1,+∞)上单调递增,在(0,1)上单调递减.
∴函数g(x0)= ![]() 的极值点为x0=0,x0=1
的极值点为x0=0,x0=1
∴关于x0方程![]() =0有三个实根的充要条件是
=0有三个实根的充要条件是
![]() ,解得-3<m<-2.
,解得-3<m<-2.
故所求的实数a的取值范围是-3<m<-2. …………… 12分


科目:高中数学 来源:2010-2011年广东省汕头市高二下学期期末考试文科数学 题型:解答题
已知函数 在x=1处取得极值,在x=2处的切线平行于向量
在x=1处取得极值,在x=2处的切线平行于向量
(1)求a,b的值,并求 的单调区间;
的单调区间;
(2)是否存在正整数m,使得方程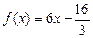 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012年河北省衡水中学高考数学信息卷5(理科)(解析版) 题型:解答题
 在x=1处取得极值2,
在x=1处取得极值2,查看答案和解析>>
科目:高中数学 来源:2010-2011年广东省汕头市高二下学期期末考试文科数学 题型:解答题
(本小题满分14分)
 已知函数
在x=1处取得极值,在x=2处的切线平行于向量
已知函数
在x=1处取得极值,在x=2处的切线平行于向量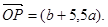
(1)求a,b的值,并求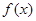 的单调区间;
的单调区间;
(2)是否存在正整数m,使得方程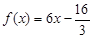 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com