
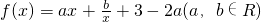 的图象在点(1,f(1)处的切线与直线y=3x+1平行.
的图象在点(1,f(1)处的切线与直线y=3x+1平行.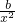 ,
,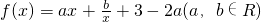 的图象在点(1,f(1)处的切线与直线y=3x+1平行,
的图象在点(1,f(1)处的切线与直线y=3x+1平行,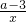 +3-2a-3lnx≥0在[1,+∞)上恒成立,
+3-2a-3lnx≥0在[1,+∞)上恒成立,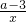 +3-2a-3lnx,x∈[1,+∞)
+3-2a-3lnx,x∈[1,+∞) -
- =
=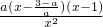 .
. ,
,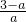 ≤l
≤l 时,g′(x)≥0,g(x)在[1,+∞)上是增函数,
时,g′(x)≥0,g(x)在[1,+∞)上是增函数, ,
,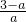 >l,
>l,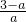 )时,g′(x)<0,g(x)在[1,+∞)上是减函数,
)时,g′(x)<0,g(x)在[1,+∞)上是减函数,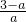 ,+∞)时,g′(x)>0,g(x)在[1,+∞)上是增函数,
,+∞)时,g′(x)>0,g(x)在[1,+∞)上是增函数,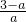 ),使得g(x0)<g(l)=0,即存在x0∈(1,
),使得g(x0)<g(l)=0,即存在x0∈(1,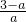 ),使得f(x0)>3lnx0不成立,
),使得f(x0)>3lnx0不成立, ,+∞).
,+∞).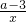 +3-2a-3lnx,x∈[1,+∞),利用导数研究g(x)的最小值,讨论a的范围,分别进行求解即可求出a的取值范围.
+3-2a-3lnx,x∈[1,+∞),利用导数研究g(x)的最小值,讨论a的范围,分别进行求解即可求出a的取值范围.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:解答题
 的图象在点(1,f(1))处的切线斜率为2.
的图象在点(1,f(1))处的切线斜率为2.查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省金华一中高三(上)期中数学试卷(文科)(解析版) 题型:解答题
 的图象在点(1,f(1))处的切线斜率为2.
的图象在点(1,f(1))处的切线斜率为2.查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省洛阳市示范高中高三联考数学试卷(文科)(解析版) 题型:解答题
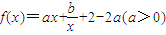 的图象在点(1,f(1))处的切线斜率为2.
的图象在点(1,f(1))处的切线斜率为2.查看答案和解析>>
科目:高中数学 来源:2012年内蒙古赤峰市元宝山二中高考数学二模试卷(理科)(解析版) 题型:解答题
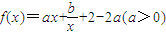 的图象在点(1,f(1))处的切线斜率为2.
的图象在点(1,f(1))处的切线斜率为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com