
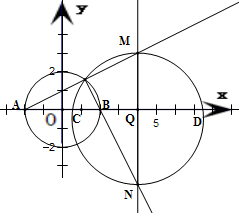
 如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.
如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.| 3 |
| 3 |
| 4|x0-4| |
| |y0| |
| 4(1-x0) |
| y0 |
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| -1 |
| k |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| y0 |
| x0+2 |
| y0 |
| x0-2 |
| 6y0 |
| x0+2 |
| 2y0 |
| x0-2 |
| 6y0 |
| x0+2 |
| 2y0 |
| x0-2 |
| 6y0 |
| x0+2 |
| 2y0 |
| x0-2 |
| 4|x0-4| |
| |y0| |
| 4(1-x0) |
| y0 |
| 4(1-x0) |
| y0 |
| 2|x0-4| |
| |y0| |
|
| 4 |
| |y0| |
| 12-3x02 |
4
| ||
| |y0| |
| 4-x02 |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
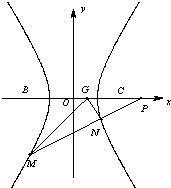 如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.| MP |
| PN |
| BC |
| GM |
| GN |
查看答案和解析>>
科目:高中数学 来源: 题型:
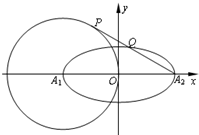 如图平面直角坐标系xOy中,椭圆
如图平面直角坐标系xOy中,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PQ |
| QA2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
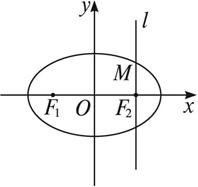
(1)求椭圆C的方程;
(2)设椭圆C的一个顶点为B(0,-b),直线BF2交椭圆C于另一点N,求△F1BN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在直角坐标系xOy中,△AiBiAi+1 (i=1,2,…,n,…)为正三角形,![]() ,|AiAi+1|=2i-1(i=1,2,3,…,n,…).
,|AiAi+1|=2i-1(i=1,2,3,…,n,…).
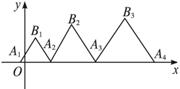
(1)求证:点B1,B2,…,Bn,…在同一条抛物线上,并求该抛物线C的方程;
(2)设直线l过坐标原点O,点B1关于l的对称点B′在y轴上,求直线l的方程;
(3)直线m过(1)中抛物线C的焦点F并交C于M、N,若![]() (λ>0),抛物线C的准线n与x轴交于E,求证:
(λ>0),抛物线C的准线n与x轴交于E,求证:![]() 与
与![]() 的夹角为定值.
的夹角为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com